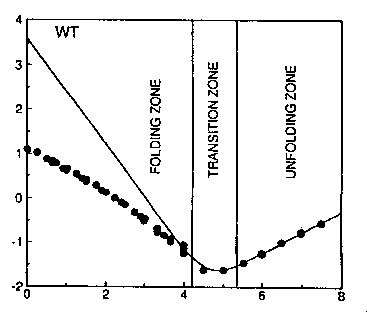
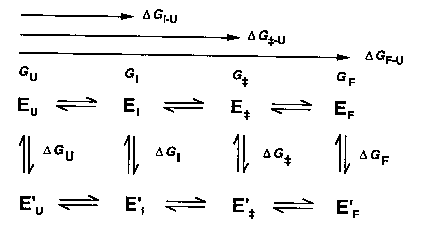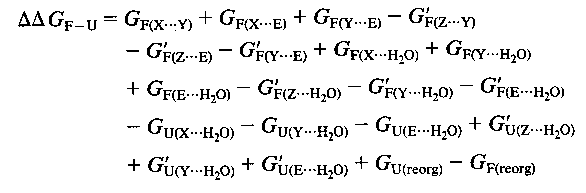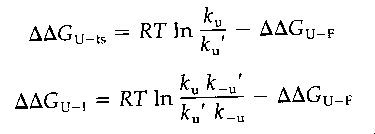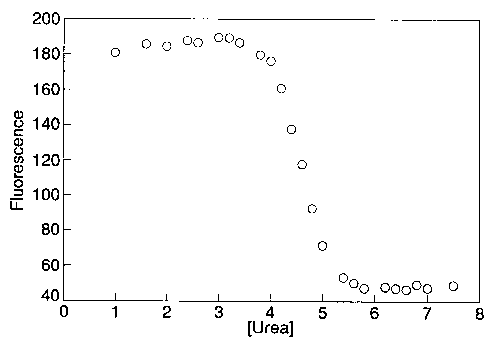A felgombolyodás vizsgálata irányított mutációk
segítségével
- Bevezetés
- Elmélet
- Reakcióséma és a látszólagos energiakülönbségek
- A valódi energiakülönbségek
- A globális energiák és az egyedi kölcsönhatások viszonya
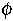 értékek
értékek
- Kétszeres mutációk ciklusai
- A felgombolyodás elemzése mutánsok segítségével
- A látszólagos energiák mérése
- Barnáz
- Egyensúlyi kísérletek barnázzal
- Kinetikai kísérletek barnázzal
- A barnáz felgombolyodása
- Értékelés
Bevezetés
- "Protein engineering" (fehérjetervezés): hatékony eszköz
- viszonylag könnyen megvalósítható (génsebészetben rutinfeladat)
- szerkezet-funkció, szerkezet-stabilitás, stb. vizsgálatok
- Felgombolyodásnál
- mutánsokat készítünk
- ezek felgombolyodását mérjük
- mindegyik mutáció az adott pozícióban zajló események próbája
- szerkezeti információt ad
- energetikai információt ad
Stratégia
- A térszerkezet alapos vizsgálatával kiválasztjuk azokat az
oldalláncokat, amelyek a stabilitásban fontos szerepet játszhatnak
- Ezeket irányított mutagenezissel módosítjuk
- Egyensúlyi és kinetikus felgombolyodási kísérleteket végzünk
- A mért paraméterek alapján felvázoljuk a mutáns és a vad típusú fehérje
ún. szabadentalpia-profilját
- Elkészítjük az energiakülönbségek diagramját
- Levonjuk a következtetéseket az egyes kölcsönhatásokról
A mutációk kiválasztása
- specifikus kölcsönhatást szüntessenek meg
- a szerkezetet a lehető legkevésbé zavarják meg
- térképezzék fel az összes fontos régiót
Kerülendő:
- komplex mutációk, melyek több kölcsönhatást befolyásolnak (nehéz
értelmezni)
- "bomlasztó", a térszerkezet átrendeződéséhez vezető mutációk (nehéz értelmezni,
felgombolyodás útvonalát is befolyásolhatják):
- nagy csoport bevitele
- új kölcsönhatásokat létesíteni képes csoport bevitele
- ellentétes töltésű párral rendelkező eltemetett töltés eltávolítása
- nagyméretű csoport eltávolítása
Elmélet
Reakcióséma és a látszólagos energiakülönbségek
Egy intermediert (I) és egy átmeneti állapotot (ts, transition
state) feltételezve:
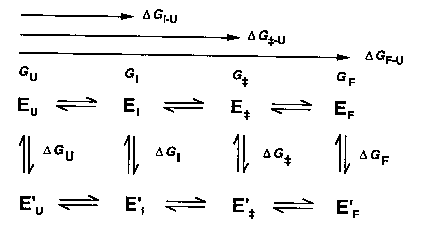
U: legombolyodott, I: intermedier, ++: átmeneti állapot, F:
felgombolyodott, vesszős: mutáns
Kísérletileg az ún. látszólagos stabilizációs energiákat
határozhatjuk meg (szabadentalpia-különbségek változása a mutáció hatására):

 GF-U =
GF-U =  GF-U -
GF-U -
 G'F-U
G'F-U

 Gts-U =
Gts-U =  Gts-U -
Gts-U -
 G'ts-U
G'ts-U

 GI-U =
GI-U =  GI-U -
GI-U -
 G'I-U
G'I-U
(Pl. a natív állapot esetében a denaturált állapothoz viszonyított
szabadentalpia eltérése a vad és a mutáns között.)
(Az "energia" alatt itt most mindig szabadentalpiát értünk!)
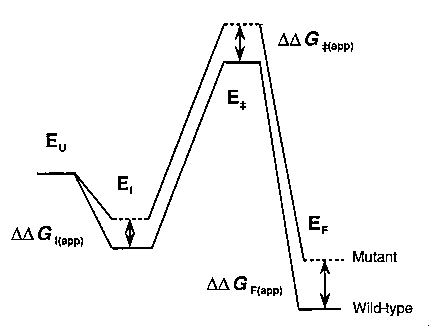
(az U állapotot referenciának vettük, ezért a vad és a mutáns diagramja
úgy van egybecsúsztatva, hogy az U szintjeik egybeessenek)
A valódi energiakülönbségek
Ami érdekel minket:az egyes állapotok szabadentalpiájának
változása a mutáció hatására ( GF,
GF,  Gts,
Gts,
 GI,
GI,  GU, vagyis a valódi
energiakülönbségek.
GU, vagyis a valódi
energiakülönbségek.
(Pl. a natív állapot esetében az állapot szabadentalpiájának változása a
mutáció hatására.)
Termodinamikai ciklusokban körbemenve az energiák előjeles összege zérus
kell legyen, ezért a fentebbi séma alapján:
 GF =
GF = 
 GF-U +
GF-U +
 GU
GU
 Gts =
Gts = 
 Gts-U +
Gts-U +
 GU
GU
 GI =
GI = 
 GI-U +
GI-U +
 GU
GU
Tehát a látszólagos energiák a konstans  GU taggal térnek
el a valódiaktól.
GU taggal térnek
el a valódiaktól.
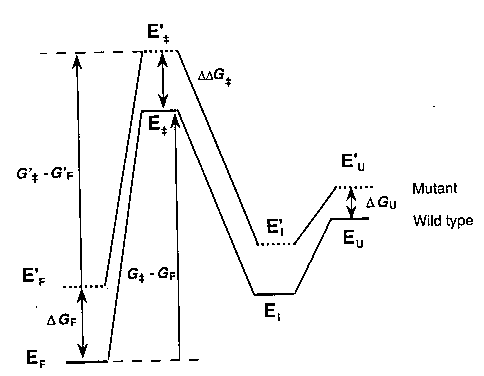
(a valódi energiaviszonyok: az U állapotok nincsenek egybecsúsztatva.
Vigyázat, itt a legombolyodott állapot bal oldalon van!)
 GU: a legombolyodott állapot szabadentalpiájának
megváltozása a mutáció hatására
GU: a legombolyodott állapot szabadentalpiájának
megváltozása a mutáció hatására
- Az U állapotot referenciának véve a
 GU-t
vehetjük mindig 0-nak
GU-t
vehetjük mindig 0-nak
- vagy: feltéve, hogy az U szerkezet nélküli, "véletlen gombolyag",
 GU a szolvatációs energiából adódik
(mérhető vagy a felszín alapján számítható)
GU a szolvatációs energiából adódik
(mérhető vagy a felszín alapján számítható)
Mivel a látszólagos energiák egy konstans taggal térnek el a valódiaktól,
egyik állapotból a másikba lépve a látszólagos energiakülönbség változása megegyezik
a valódi energiakülönbség-változással!
A globális energiák és az egyedi kölcsönhatások viszonya
A mért (látszólagos) 
 G-k a
teljes molekulára vonatkozó, globális mennyiségek. Hogyan függenek
össze az egyedi kölcsönhatások energiáival?
G-k a
teljes molekulára vonatkozó, globális mennyiségek. Hogyan függenek
össze az egyedi kölcsönhatások energiáival?
A globális G-hez (a molekula teljes szabadentalpiájához) való
hozzájárulások két csoport (X és Y) kölcsönhatása esetén:
- X és Y kölcsönhatása egymással
- X és Y kölcsönhatása a fehérje többi részével (E-vel)
- X és Y kölcsönhatása az oldószerrel
- E kölcsönhatása az oldószerrel
Az egyik csoport kicserélésére (X-->Z) mindezek megváltoznak, továbbá
- a szerkezet átrendeződhet (reorg)
Ezek a mennyiségek pedig eltérőek az U és F állapotban.
Mindent összegezve a stabilizációs szabadentalpia megváltozása az
X-->Z mutáció hatására:
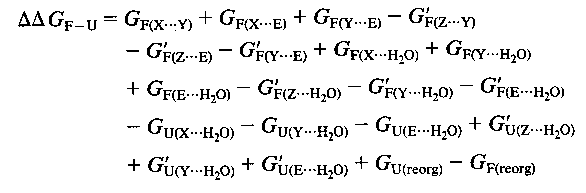
(legáltalánosabb eset)
Egyszerűsítések
A fenti egyenlet speciális esetekben egyszerűsíthető:
- Nem bomlasztó mutáció esetén: a
 Greorg tagok
kiesnek, Y kölcsönhatásai E-vel és a vízzel ugyanazok a vad és mutáns fehérjében
Greorg tagok
kiesnek, Y kölcsönhatásai E-vel és a vízzel ugyanazok a vad és mutáns fehérjében
- Deléció (csoport eltávolítása) a víz számára nem hozzáférhető helyen:
oldószeres tagok nagy része kiesik, Z...Y kölcsönhatás kiesik
- Deléció a víz számára hozzáférhető helyen: az X...Y kölcsönhatást
víz...Y váltja fel, Z...Y nincs
- Helyettesítés (az eredetivel megegyező méretű csoporttal)
- Izosztérikus helyettesítés (az eredetivel megegyező geometriájú
csoporttal, pl. Val-->Thr)
(3-4 tagú egyenletek)
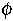 értékek
értékek
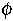 : RELATÍV DESTABILIZÁCIÓ. Az S (tetszőleges)
állapotra (S lehet az U, az I, a ts vagy az F):
: RELATÍV DESTABILIZÁCIÓ. Az S (tetszőleges)
állapotra (S lehet az U, az I, a ts vagy az F):
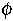 S =
S = 
 GS-U/
GS-U/
 GF-U
GF-U
0 és 1 közé esik. Jelentése: a mutáció mennyire destabilizálja az S állapotot,
az F állapot destabilizációjához viszonyítva.
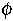 =1: az S állapotot ugyanúgy érinti a mutáció, mint az F-et. Tehát a
mutáció által elvett kölcsönhatás S-ben is megvan.
=1: az S állapotot ugyanúgy érinti a mutáció, mint az F-et. Tehát a
mutáció által elvett kölcsönhatás S-ben is megvan.
- (vagy: nincs meg, de ugyanakkora energiájú másik kölcsönhatás jön létre)
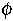 =0: az S állapotot nem érinti a mutáció. Tehát a mutáció által elvett
kölcsönhatás S-ben nincs meg.
=0: az S állapotot nem érinti a mutáció. Tehát a mutáció által elvett
kölcsönhatás S-ben nincs meg.
- 0<
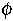 <1:
<1:
- az S állapotban részlegesen van meg a kölcsönhatás, vagy
- a molekulák egy részében megvan, más részében nincs
Feltevések
A bemutatott elemzés feltételei:
- A mutáció nem változtatja meg a felgombolyodás útvonalát
(Gts,reorg és GI,reorg elhanyagolható)
- A mutáció nem változtatja meg jelentősen sem a felgombolyodott, sem a
legombolyodott állapot szerkezetét (GF,reorg, GU,reorg elhanyagolható)
- A vizsgált csoport a felgombolyodás során nem létesít más csoportokkal
más kölcsönhatásokat, mint a natív szerkezetben
- A legombolyodás ugyanazon az úton történik, mint a felgombolyodás, csak
visszafelé [ez némely esetben igazolható]
Kétszeres mutációk ciklusai
Az egyszeres mutációk problémái:
- Nem derül ki, ha a csoport a felgombolyodás során más csoporttal létesít
kölcsönhatást, mint a natív állapotban
- A csoportok kölcsönhatása a fehérje többi részével bonyolítja az elemzést
Hogyan vizsgálható közvetlenül két csoport kölcsönhatása? Kettős mutációs
ciklussal!
Négy változatot vizsgálunk:
- vad típus E-XY
- egyszeres mutáns Y-ban: E-X
- egyszeres mutáns X-ben: E-Y
- kettős mutáns: E
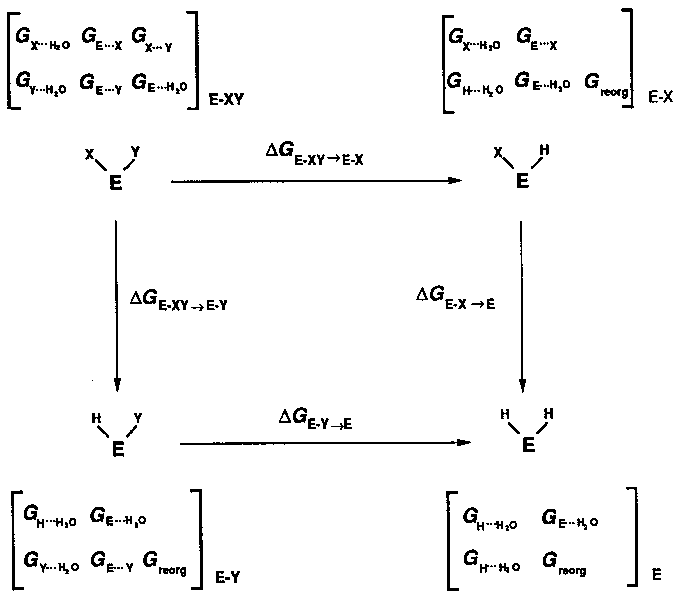
(szögletes zárójelben az egyes állapotok szabadentalpiájában szerepet
játszó tagok)
Kölcsönhatási energia ( Gint): mennyivel módosul az
egyik mutáció hatása, ha a másik mutáció is megvan:
Gint): mennyivel módosul az
egyik mutáció hatása, ha a másik mutáció is megvan:

 Gint =
Gint = 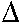 GE-XY->E-X -
GE-XY->E-X - 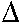 GE-Y->E =
GE-Y->E = 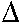 GE-XY->E-Y -
GE-XY->E-Y - 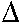 GE-X->E
GE-X->E
Hogy adható meg a kölcsönhatási energiákkal?
Ha a mutáció nem bomlasztó, a reorganizációs tagok elhanyagolhatóak, más
tagok kiesnek, így

 Gint = GX...Y -
Gint = GX...Y -
 GX...víz -
GX...víz -  GY...víz
GY...víz
tehát az X...Y kölcsönhatás és a szolvatációs tagok különbsége.
Ha a víz nem fér hozzá a mutált helyhez, akkor

 Gint=GX...Y
! (maga a kölcsönhatási energia!)
Gint=GX...Y
! (maga a kölcsönhatási energia!)

 Gint bármely S állapotra kiszámítható
(
Gint bármely S állapotra kiszámítható
(
 GS,int)
GS,int)
- Relatív kölcsönhatási energia:
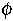 S,int=
S,int=
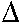 GS,int/
GS,int/
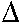 GF,int:
azt mondja meg, hogy az S állapotban milyen mértékben van meg az adott
kölcsönhatás, a felgombolyodott állapothoz képest.
GF,int:
azt mondja meg, hogy az S állapotban milyen mértékben van meg az adott
kölcsönhatás, a felgombolyodott állapothoz képest.
- kiterjeszthető magasabb dimenziókra: hármas mutáns ciklusok, stb.
(kölcsönhatások kooperativitásának tesztelése)
A felgombolyodás elemzése mutánsok segítségével
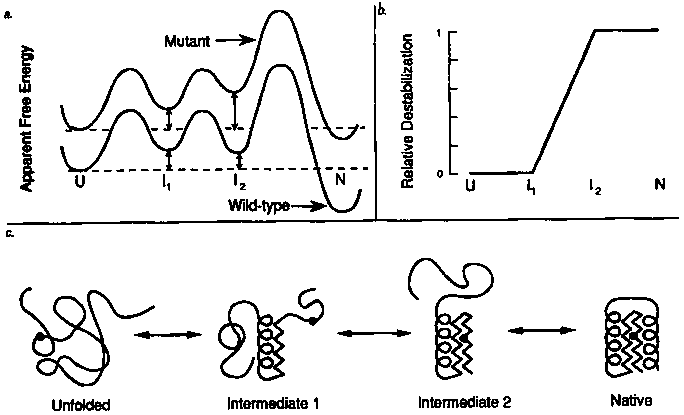
(a kölcsönhatás az U és I1 állapotokban nincs meg, az
I2 és N állapotokban megvan
- Elkészítjük a vad és a mutáns fehérje szabadentalpia-profilját (a)
- Kiszámítjuk az egyes állapotok
 értékeit (b)
értékeit (b)
- A
 -diagramból következtetünk a kölcsönhatás
jelenlétére a felgombolyodás folyamatának egyes állomásain
-diagramból következtetünk a kölcsönhatás
jelenlétére a felgombolyodás folyamatának egyes állomásain
Példák:
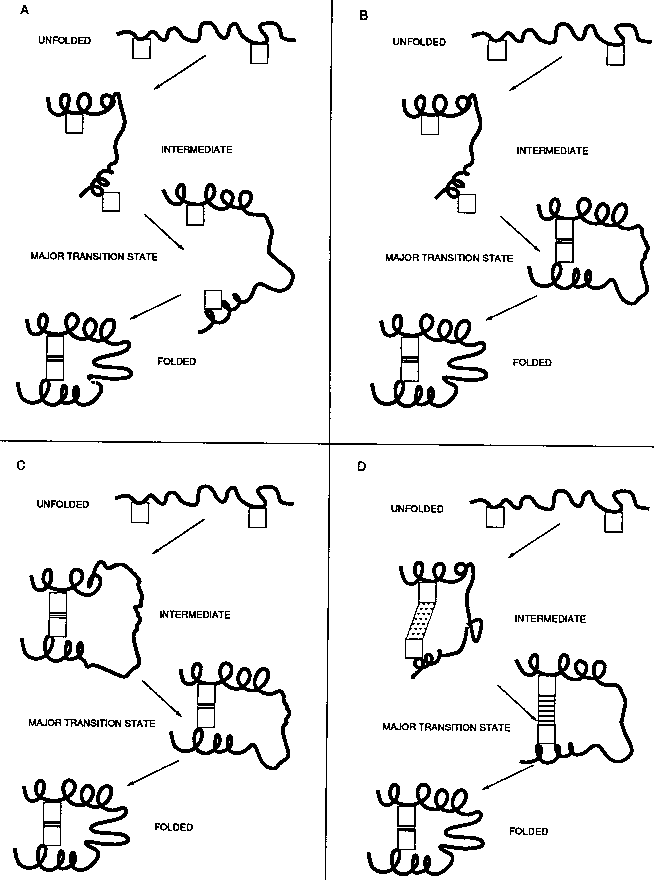
Lehetséges forgatókönyvek (mely fázisban jön létre a kölcsönhatás)
- (a) csak F-ben
- (b) ts-ben
- (c) már I-ben
- (d) I-ben gyengén, ts-ben erősebben, de teljesen csak F-ben
A látszólagos energiák mérése
Hogyan mérjük meg a 
 -mennyiségeket?
-mennyiségeket?
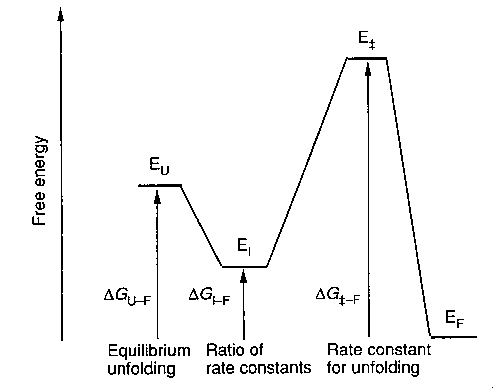
- A felgombolyodott állapotra vonatkozó látszólagos energia egyensúlyi
denaturációból származtatható (vadra és mutánsra)
- Az átmeneti állapotra vonatkozó látszólagos energiák a legombolyodás
sebességi állandójából számíthatóak (mutánsra és vadra megmérve)
- Az intermedierekre vonatkozó látszólagos energiák a le- és
felgombolyodás sebességi állandóinak hányadosából számíthathatóak (mutánsra
és vadra megmérve)
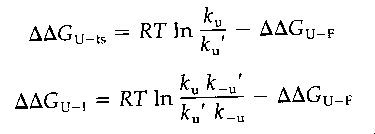
(kuaz F-I átmenet, k-u az I-F átmenet sebességi
állandója)
A 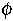 értékek:
értékek:
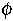 I =
I =

 GI-U/
GI-U/
 GF-U
GF-U
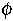 ts =
ts =

 Gts-U/
Gts-U/
 GF-U
GF-U
Barnáz
- Bacillus amyloliquefaciens
ribonukleáz
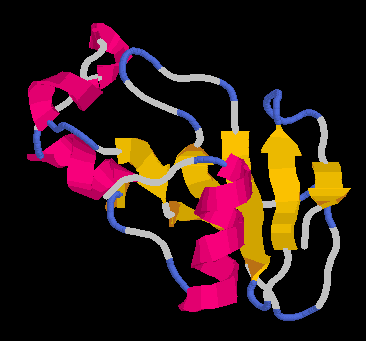
110 aminosav, 3 hélix, egy ötszálú antiparallel béta-lemez
- Részletes szerkezet:
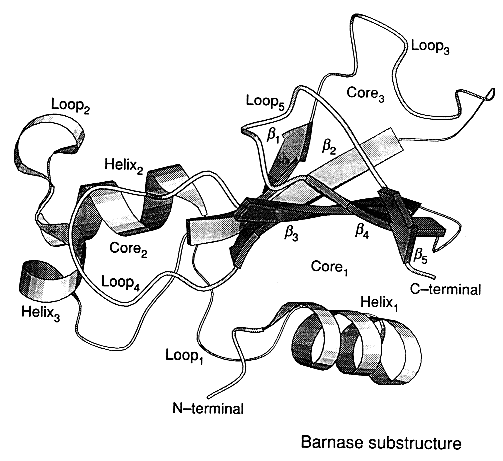
- hélix1 (leghosszabb): béta lemezzel core1
hidrofób mag
- lemez másik oldalán loop3 és loop5 hurokrégiók a
béta-lemezzel képezik a core3 hidrofób magot
- hélix2 és hélix3 a lemez élével képezik a
core2 hidrofób magot
- aktív helyet a loop3 és loop5 közti hasadék képezi
- Jó tulajdonságai:
- Denaturálószerrel és hővel reverzibilisen denaturálható
- Egyensúlyi fel/legombolyodása kétállapotú
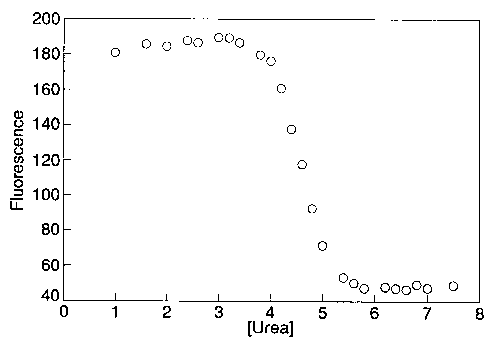
- Nincs benne cisz-prolin
Egyensúlyi kísérletek barnázzal
Az egyes kölcsönhatások szerepének feltérképezése: több mint 60 mutáns
elemzésével (Alan Fersht és mtsai, Cambridge)
Elektrosztatikus kölcsönhatások
- Felszíni középtávúak (<10 angström): igen kicsi a járulékuk.
- Rövidtávúak (<3,5 angström): csekély a járulékuk: 0,3-1 kcal/mol
- Eltemetett ionpárok: egyik töltést eltávolítva nagy destabilizáció (3-4
kcal/mol)
- (magas hőmérsékleten nagyobb lehet a felszíni ionpárok stabilizáló
hatása is! ld. termofil fehérjék)
Hidrogénkötések
Háromféle mutáció:
- A hidrogénkötésben részt vevő csoport eltávolítása (pl. Ser->Ala,
Tyr->Phe)
- Felszínen: destabilizáció < 0,5 kcal/mol
- Eltemetett, töltetlen csoportok között: destabilizáció 1-1,5 kcal/mol
- Eltemetett, töltött csoportok között: destabilizáció 3-4 kcal/mol
- Nagyobb rész eltávolítása (pl. Asp, Gln, Asn -> Ala):
más kölcsönhatásokat is befolyásol. Destabilizáció: 2-3 kcal/mol
Hidrofób kölcsönhatások
- Egy eltemetett metil(én)csoport eltávolítása átlag 1,5 kcal/mol
destabilizációt okoz
- A destabilizáció arányos az eltávolított csoporttól 6 angströmnél nem
messzebb lévő metil(én)csoportok számával:
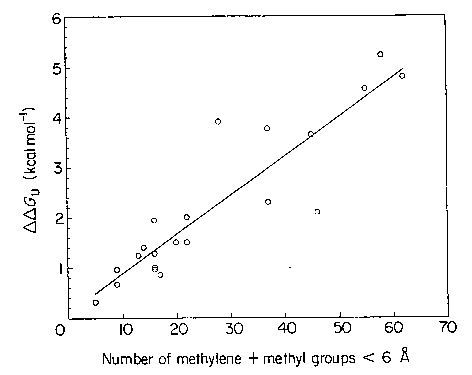
- A destabilizáció annál nagyobb, minél jobb az eredeti térkitöltés
A hidrofób kölcsönhatás adja a legnagyobb járulékokat, a hidrogénkötések
és az elektrosztatikus kölcsönhatások viszont a natív szerkezet
specificitásában játszanak nagy szerepet.
Kinetikai kísérletek barnázzal
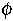 -elemzések:
Több mint 40 mutáns segítségével elemezték a felgombolyodás folyamatát
(Fersht). Ötféle mutáns:
-elemzések:
Több mint 40 mutáns segítségével elemezték a felgombolyodás folyamatát
(Fersht). Ötféle mutáns:
- hélixekben (dupla mutációs ciklusok is)
- béta-szálakban
- béta-kanyarokban
- hidrofób magokban
- hurkokban
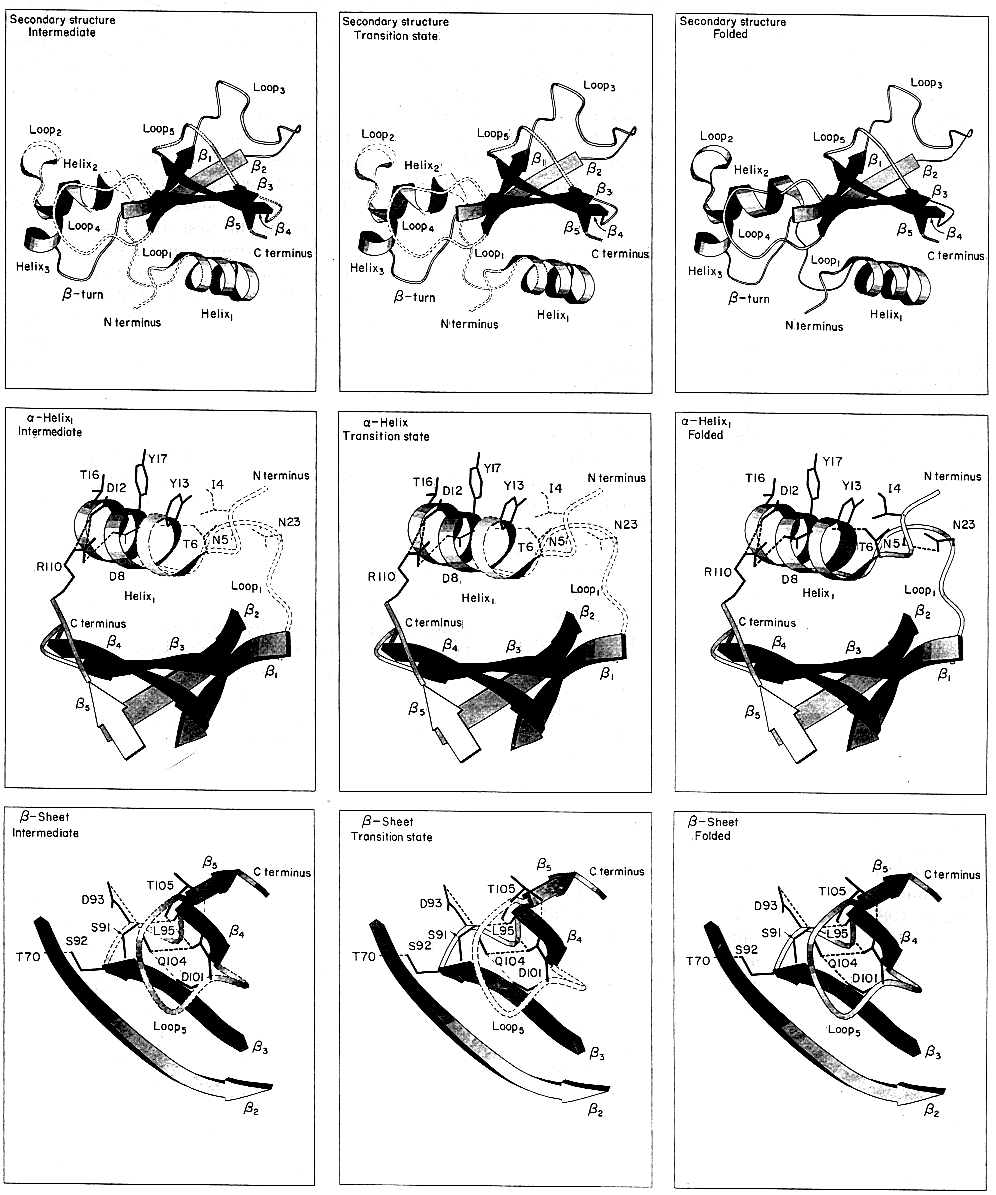
A barnáz felgombolyodása
Hidrofób magok
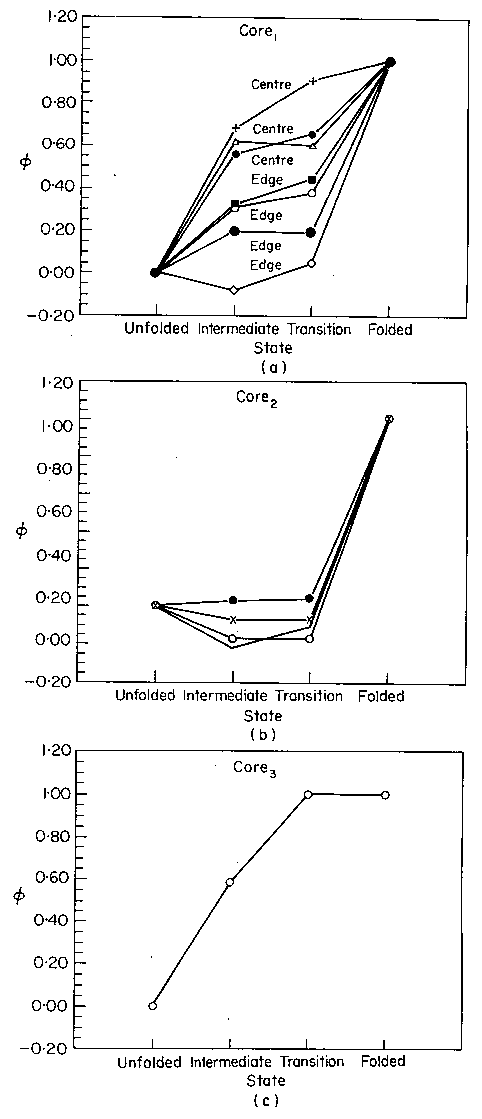
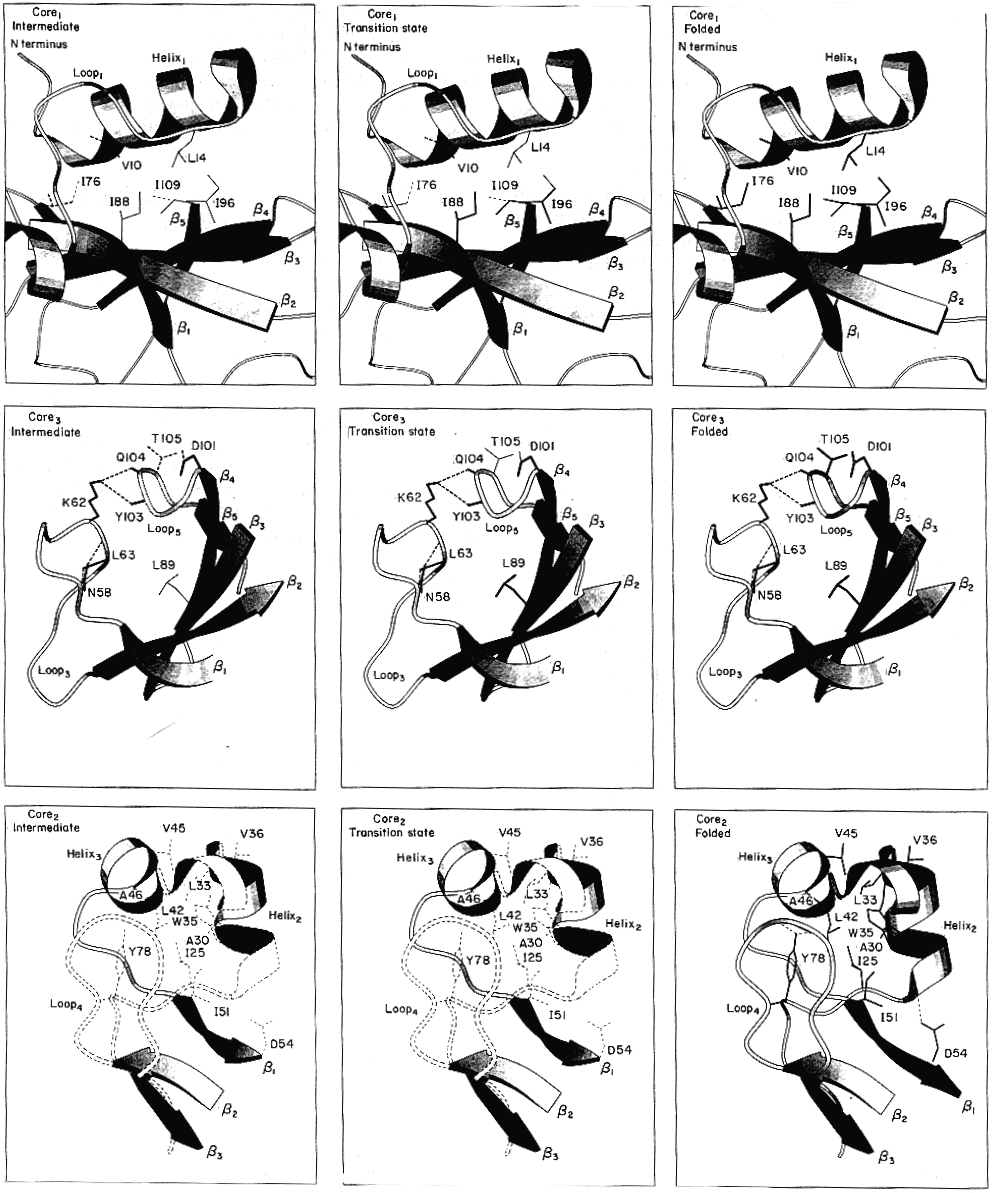
(bal: I áll., közép: ts áll., jobb: natív
szaggatott vonal: legombolyodott; vékony: részleges; vastag: felgombolyodott)
- A core1 mag az I állapotban elkezd kialakulni, ts-ben
megerősödik. A közepe előbb megjelenik és erősebb, mint a széle.
- A core2 mag csak a ts állapot után alakul ki
- A core3 mag az I állapotban elkezd kialakulni, ts-ben már
kompakt
Hurkok:
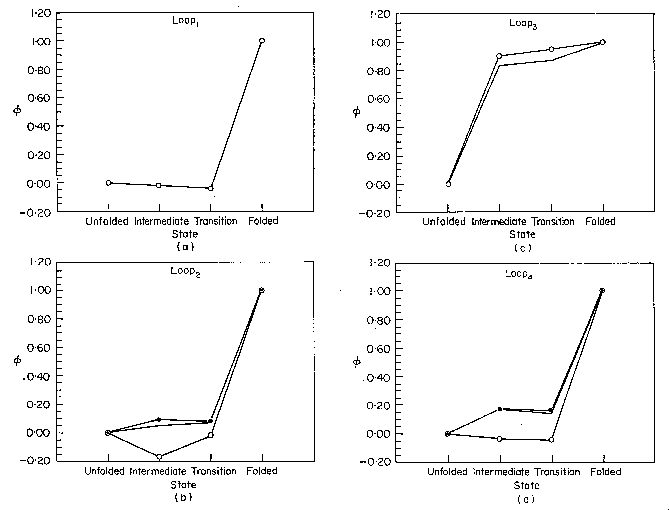
- A loop2, loop4 és a loop1 egy része
csak a ts állapot után alakul ki
- A loop3 (szubsztrátkötő) már az I állapotban kialakul, a
loop5 is részlegesen
Béta-szerkezet
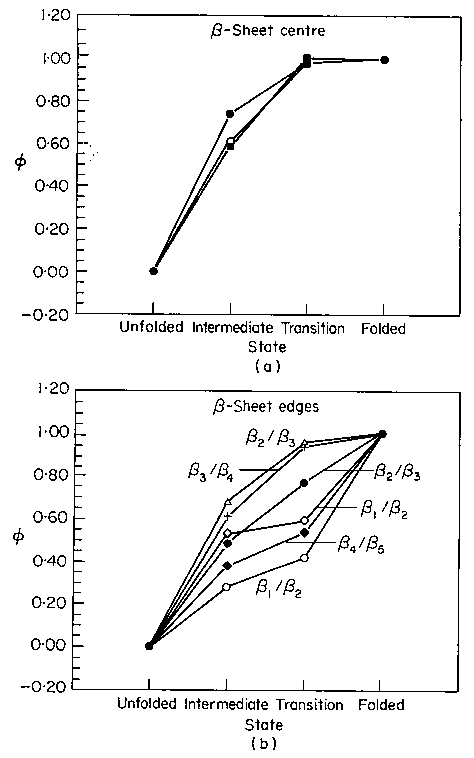
- A béta-lemez közepe az I állapotban lényegében kialakult, de a szélei
gyengék
Hélixek
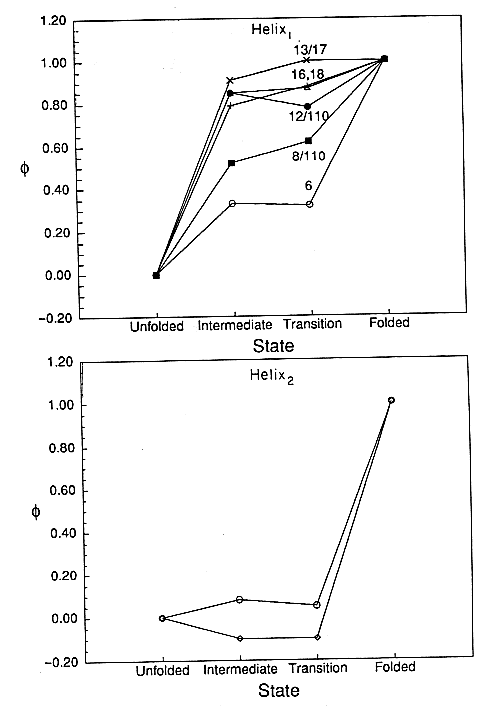
- A hélix1 N-terminális egyharmada az I állapotban laza, a
maradék kétharmad rész viszont már lényegében megvan
- A hélix2 csak a ts állapot után alakul ki
Értékelés
- Mutánsok elemzésével meglepően pontos képet lehet kapni a felgombolyodás
folyamatáról
- A mutációs elemzésből kapott eredményeket összehasonlították az NMR-rel
követett hidrogénkicserélődési mérések eredményeivel
- Az egyezés jó
- A mutációs elemzés elsősorban az oldalláncokról ad információt
- A hidrogénkicserélődés elsősorban a gerincről ad információt
- Együttesen alkalmazandó, komplementer módszerek
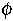 értékek
értékek