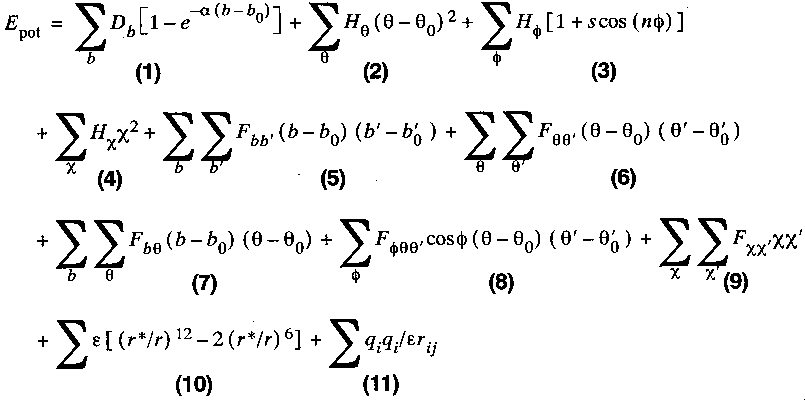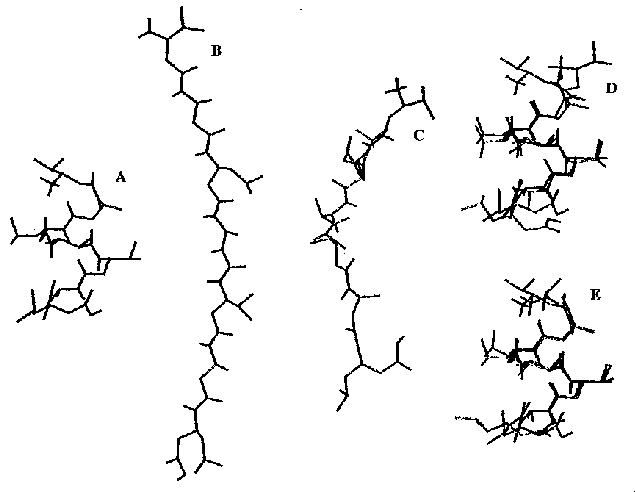A fel- és legombolyodás molekuladinamikai szimulációi
1. Mi a molekuladinamika?
2. Modern módszerek a molekuladinamikában
3. Peptidek vizsgálata MD-vel
4. Fehérjék natív szerkezetének MD szimulációi
5. A legombolyodás MD szimulációi
6. A felgombolyodás MD szimulációi
Mi a molekuladinamika?
A potenciálisenergia-felület
- Born-Oppenheimer-közelítés: az elektronok mozgása sokkal gyorsabb az
atommagokénál, ezért a Schrödinger-egyenlet két külön egyenletre esik szét.
Az első az elektronokra vonatkozó Schrödinger-egyenlet, amely paraméteresen
függ az atommagok R pozícióitól. Ennek megoldása adja az E(R)
potenciálisenergia-függvényt, amely csak az atommagok pozícióitól függ. A
második egyenlet az atommagok mozgását írja le ezen az E(R)
potenciálfelületen.
- Az E(R) potenciálfüggvényt empirikus energiafüggvénnyel
helyettesíthetjük (a Schrödinger-egyenlet megoldása helyett)
- Az atommagok nehezek, a rájuk vonatkozó Schrödinger-egyenlet helyett
használhatjuk a Newton-féle mozgásegyenletet:
-(dE/dR) =
m(d2R/dt2)
Ez a molekuladinamika, röviden MD.
A forcefield
- A forcefield az empirikus energiafüggvény matematikai alakja. Egy
tipikus forcefield:
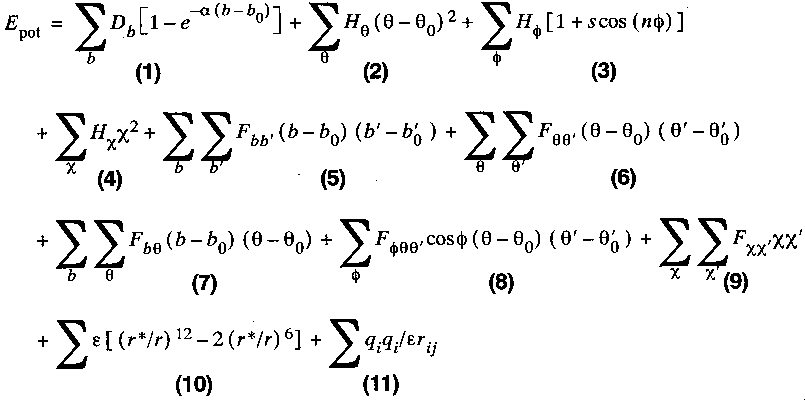 Az egyes tagok jelentése:
Az egyes tagok jelentése:
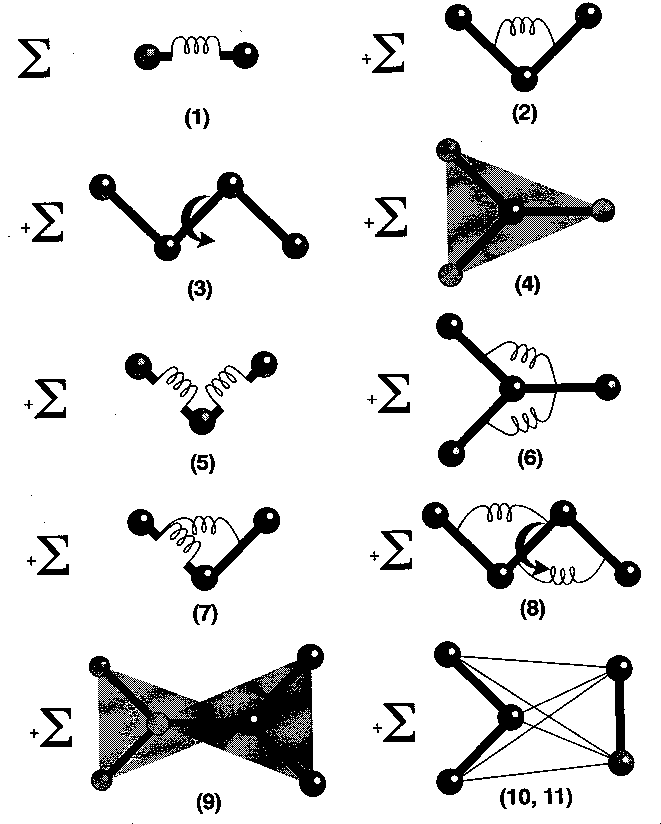
- 1. kötések nyújtása (Morse-potenciál vagy egyszerű harmonikus potenciál)
- 2. kötésszögek változtatása
- 3. torziós szögek változtatása
- out-of-plane kölcsönhatások (atom kitérése sík csoportból)
- 5-9. kereszttagok (csatolások az 1-4. effektusok között)
- 10. Van der Waals
- 11. Coulomb
- A képletben szereplő paraméterek értékét empirikus adatok (pl.
kristályszerkezet, rácsdinamika, röntgenadatok, sűrűség, párolgáshő, stb.)
alapján illesztik, néha ab initio kvantumkémiai számítások
eredményeit is felhasználják.
- Az empirikus adatok miatt a forcefield implicit módon magában foglalja a
relativisztikus és kvantummechanikai effektusokat is.
- Ismertebb forcefieldek fehérjékhez: AMBER, CHARMM, ECEPP, GROMOS, CVFF
A párkölcsönhatások problémája
- A párkölcsönhatások száma négyzetesen nő a rendszer méretével, ez nagyon
megnöveli az energiafüggvény kiértékeléséhez szükséges időt.
- Megoldás: cutoff (határtávolság) alkalmazása: a cutoffnál (10-20
angström) messzebb lévő párok kölcsönhatását nem vesszük figyelembe
- Problémák: cutoff sokféle hibát okoz
- Nem hirtelen levágás, hanem fokozatos lecsengetés javít valamit.
- Elektrosztatikus kölcsönhatások energiája 1/r-es, vagyis csak lassan
csökken. Megoldások:
- Töltéscsoportok bevezetése. Egymáshoz közeli, kb. zérus
össztöltésű csoportokat jelölünk ki. Ha bármelyik atom belül van a cutoffon,
akkor már a többit is figyelembe vesszük.
- Cell Multipole Method: a rendszert kockákra bontjuk és az
ezekben lévő atomok potenciálját multipól sorfejtéssel közelítjük. Nincs
cutoff, távoli kockák potenciálja is számít.
- Ewald-összegzés: (a potenciál egy részét a reciprok rácson
számítja ki)
Az oldószer modellezése
- Explicit: vízmolekulákkal körülvesszük a vizsgált molekulát (néhány
réteg vagy egy feltöltött doboz (periodikus határfeltétellel))
- Implicit: a potenciált módosítjuk, pl. távolságfüggő dielektromos
állandó, kétféle dielektromos állandó (a fehérje belsejére, ill. a rajta
kívül lévő térre), stb.
Eljárások
Energiaminimalizálás
- Cél: a potenciálfelület minimumainak megkeresése (ezek körül fluktuál a
konformáció). Modellszerkezetek optimalizálására is jó.
- Legmeredekebb esés módszere: mindig az energiafelület
deriváltjának irányába lépünk.
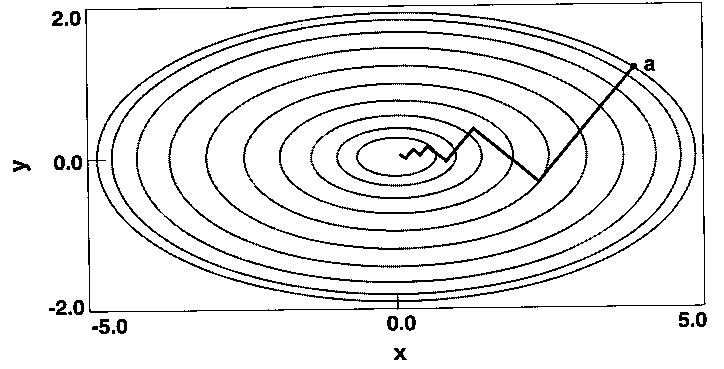
Az energiaminimumtól távol jól konvergál, hozzá közel rosszul.
- Konjugált gradiensek módszere: a lépésirányt az előző lépések deriváltjainak felhasználásával korrigáljuk. Az i+1. ponthoz vezető lépés irányvektora:
hi+1 = gi+1 + khi,
ahol gi+1 a gradiens az i+1. pontban, k pedig egy állandó, aminek az értéke a Polak-Ribiere módszerben k=(gi+1gi+1)/ (gigi), a Fletcher-Reeves-módszerben k=((gi+1-gi) gi+1)/ (gigi). Tehát a gradiens mindig ortogonális az előző gradiensekre, az irányok pedig konjugáltak az előző irányokra. Ez a módszer nagy rendszereknél és a minimumok közelében is gyorsan konvergál.
- Newton-Raphson-módszerek: a potenciálfüggvény második deriváltját, azaz görbületét is felhasználják. Ha a felület kvadratikus függvény lenne, ez egy lépésben a minimumba vezetne. A második deriváltak mátrixának kiszámítása időigényes, a mátrix helyigényes, ezért a módszer csak kis molekuláknál használható, ráadásul a minimumtól távol instabil (divergálhat).
Molekuladinamika
- Cél: a rendszer dinamikájának feltárása, konformációs mozgások szimulálása
- dt lépésköz: 1-2 femtoszekundum
- Verlet-féle bakugrás módszere: a t időpontban mérhető
erőből (f(t)) kiszámítjuk a gyorsulást (a(t)), ezzel pedig a t-(1/2)dt időpontbeli sebességből a t+(1/2)dt időpontbeli sebességet (v(t+(1/2)dt) = v(t-(1/2)dt) + dta(t). A sebesség felhasználásával az r(t) t időpontbeli helyvektorból kapjuk a t+dt időpontbeli helyvektort: r(t+dt) = r(t) + dtv(t+(1/2)dt). Bakugrás-módszer, mert a sebesség mindig fél lépésközre jár a pozíciótól. (Ez a hátránya.)
- Verlet-féle sebességi módszer: nincs elcsúszás, a t+dt időpontbeli pozíció: r(t+dt) = r(t) + dtv(t)+(1/2)dt2a(t)
- A Verlet-módszerek a legkedvezőbbek, mert lépésenként csak 1 energiaszámítást igényelnek, nem memóriaigényesek, nagy lépésközt tesznek lehetővé.
A hőmérséklet beállítása
- A kezdeti sebességeket az adott hőmérsékletnek megfelelően véletlenszerűen generáljuk Maxwell-Boltzmann eloszlás szerint
- A rendszer hőmérséklete bármely pillanatban a kinetikus energiából számítható: T = 2K/(NfkBT), ahol K = szumma (1/2)mv2 a kinetikus energia, Nf a szabadsági fokok száma, kB a Boltzmann-állandó
- Direkt sebességskálázás: a sebességek közvetlen beállítása a célhőmérsékletre bármikor, amikor eltér attól, egy tényezővel való beszorzás révén. Dinamika kezdeti szakaszában szokásos.
- Hőtartályhoz csatolás (Berendsen-módszer): Bevezetjük a tau relaxációs időt, ez a hőmérséklet kiegyenlítődésének relaxációs ideje. Az atomi sebességeket a következő tényezővel skálázzuk: [1 + (dt/tau)(Tpillanatnyi - Tcél)]1/2. Jó közelítéssel állandó hőmérsékletre jellemző statisztikai sokasághoz (kanonikus sokasághoz) vezet.
- Újabb módszerek: Nosé-Hoover termosztát (kanonikus sokaságot ad), Andersen-módszer (sebességek véletlenszerű újraelosztása)
A nyomás beállítása
- "Nyomástartályhoz" csatolás (Berendsen-módszer): hasonló a hőtartályos Berendsen-módszerhez, de nem a sebességeket, hanem az atomi koordinátákat skálázzuk
Kényszerek alkalmazása
- Kötéshosszak és kötésszögek állandó értéken tartásával a lépésköz növelhető 2-10 fs-ra
- Többféle algoritmus, jósági sorrendben: SHAKE, RATTLE, LINCS (legjobb)
Modern módszerek a molekuladinamikában
Többszörös lépésköz (multiple time step)
- Hosszútávú kölcsönhatások lassabban változnak --> nem szükséges minden lépésben újraszámolni őket
- Kétféle lépésköz: a hosszútávú kölcsönhatásokra egy nagyobb, a rövidtávúakra egy kisebb
- Többféle megvalósítás, a nagyobb lépésköz 4-48 fs között változik
- Még nem kiforrott, különféle problémák vannak
- A jövőben a szükséges gépidő akár egy nagyságrenddel is csökkenhet e módszer révén
Esszenciális dinamika (Berendsen)
A fehérjemolekulák belső mozgásainak típusai
| A mozgás típusa | Térbeli kiterjedés
(angström) | Amplitúdó
(angström) | Jellemző időskála
|
|---|
| Kötések rezgései | 2-5 | 0,01-0,1 | 10-100 fs
|
| Globuláris régiók rugalmas deformációi | 10-20 | 0,05-0,5 | 1-10 ps
|
| Felszíni oldalláncok rotációja | 5-10 | 5-10 | 10-100 ps
|
| Eltemetett csoportok torziós rezgései | 5-10 | 0,5 | 10 ps - 1 ns
|
| Globuláris domének relatív mozgásai | 10-20 | 1-5 | 10 ps - 100 ns
|
| Belső oldalláncok rotációja | 5 | 5 | 100 mikrosec - 1 s
|
| Allosztérikus átmenetek | 5-40 | 1-5 | 10 mikrosec - 1 s
|
| Lokális legombolyodás | 5-10 | 5-10 | 10 mikrosec - 10 s
|
- A molekuláris mozgások egy része csupán gyors, harmonikus rezgőmozgás, ami voltaképpen érdektelen
- Az esszenciális dinamika módszere:
- Végzünk egy pár száz pikoszekundumos normál molekuladinamikát
- A dinamika eredményéből kiszámítjuk az ún. elmozdulási korrelációs mátrixot
(a koordináták második momentumainak mátrixa, az egyes atompárok mozgásának
korrelációját adja meg),
s ezt átlagoljuk a futtatott dinamikára (<uiuj>).
- A mátrix sajátvektorai a koordináták lineáris kombinációi, az ún. kollektív
koordináták
- A mátrix sajátértékei az egyes kollektív koordináták mentén vett átlagos
fluktuációk mértékei
- Ált. a 10 legnagyobb sajátérték (és a hozzájuk tartozó sajátvektorok) a
fehérje összes lényeges, nagy amplitúdójú mozgásait leírja
- Ezután szimulációt végzünk csak ezen esszenciális koordinátákra; a többi koordinátával csak harmonikus rezgőmozgást végeztetünk
- Vizsgálatok szerint a módszer jelentősen megnöveli a konformációs térnek az adott idő alatt szimulációval felderíthető részének méretét
A molekuladinamika korlátjai
- A számítógépek jelenlegi teljesítőképessége mellett a szimulálható
időtartam korlátozott. Fehérjemolekulán az eddigi rekord 1 mikroszekundum
szimulációja (1 hónapig tartott egy 256 processzoros szuperszámítógépen).
Korszerű módszerekkel ez még növelhető kb. egy nagyságrenddel
- A klasszikus mechanikai modell nem alkalmas kémiai események
szimulálására (pl. ionizáció, protontranszfer, stb.)
Mire használható a molekuladinamika?
- Szerkezetfinomítás: még tökéletlen minőségű modellszerkezetek
finomíthatóak vele
- Szerkezetjóslás: mutáns fehérje szerkezete jósolható (kicseréljük
az oldalláncot, majd molekuladinamikával relaxáljuk a szerkezetet).
- Dokkolás: ligandum v. szubsztrát kötődési helyének megtalálása
egy fehérje felszínén (kevésbé megbízhatóan)
- Fehérjemolekulák fontos funkcionális mozgásainak feltérképezése:
pl. domének relatív mozgásai enzimkatalízis során, stb. (kevéssé megbízhatóan)
- Fehérjemolekulák le- és felgombolyodásának szimulációi: a
mechanizmus felderítése céljából
Peptidek vizsgálata MD-vel
Egy héttagú béta-peptid
(Daura et al., JMB 280:925 (1998))
Tehát: a szimuláció jól megtalálta a natív szerkezetet, és leírja a
natív-denaturált állapotok közötti hőmérsékletfüggő egyensúlyt.
Egy helikális és egy béta-hajtű konformációjú peptid
szimulációja
(Schaefer et al., JMB 284:835 (1998))
Helikális peptid
- Ribonukleáz A C-terminális hélixének felel meg
- 13 aminosav: AETAAAKFLRAHA
- Kísérlet (CD): oldatban, 3 Celsius-fokon 50-60% hélix
Béta-hajtű
- Tervezett hajtűkonformáció
- 12 aminosav: RGITVNGKTYGR
- Kísérlet (CD, NMR): 274 K-en 19-37% béta-hajtű
Szimulációk:
- Indulás: nyújtott konformáció
- Forcefield: ACS - Analytical Continuum Solvent: implicit oldószer, egy
dielektromos állandóval és egy apoláros szolvatációs állandóval. Effektív
szabadenergiát ad.
- Ún. esernyő-mintavételi technika (hőmérséklet változtatásának felel meg)
- 10 ns szimulációk
Eredmények
- Az effektív szabadenergia, a hélixtartalom és a bétahajtű-tartalom
változása az idő függvényében:
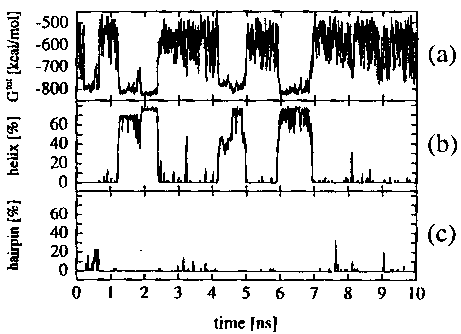
(A helikális peptidre)
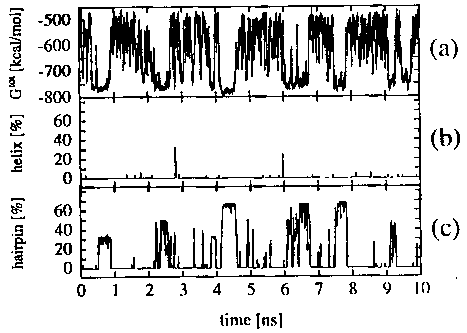
(A hajtűpeptidre)
- Mindkét peptid a neki megfelelő konformációt preferálja
- Több átmenet, egyensúly áll be
- Számítás: a helikális peptid 58% hélix, a hajtűpeptid 38% hajtű
- 2% körüli valószínűséggel a másik konformációt is felveszik!
Tehát: rövid peptidek felgombolyodása molekuladinamikával jó
eredménnyel szimulálható.
Fehérjék natív szerkezetének MD szimulációi
Kérdések:
- A natív állapoton belül milyen alállapotok között fluktuál a konformáció?
- A molekuladinamika képes-e ésszerű időn belül megfelelő mintát venni a
natív konformációk halmazából?
BPTI (bovine pancreatic trypsin inhibitor) szimulációja
(Troyer és Cohen, Proteins 23:97 (1995))
- BPTI: 58 aminosav, egy béta-lemez és egy hélix, 3 diszulfidhíd
- Szimuláció: 1 ns, explicit oldószerrel
- Energiaminimalizálások: Az MD-trajektória egyes pontjaiban (azaz a
szimuláció egyes időpontjaiban) előálló
szerkezeteket minimalizálták, az energiafüggvény lokális minimumainak
feltárása végett
- Klaszteranalízis: az MD, ill. az energiaminimalizálások révén nyert
konformációkat szerkezeti hasonlóság alapján csoportosítják
Eredmények:
- RMSD mátrix (a szimuláció során fellépő konformációk párjai közötti
RMSD-k):
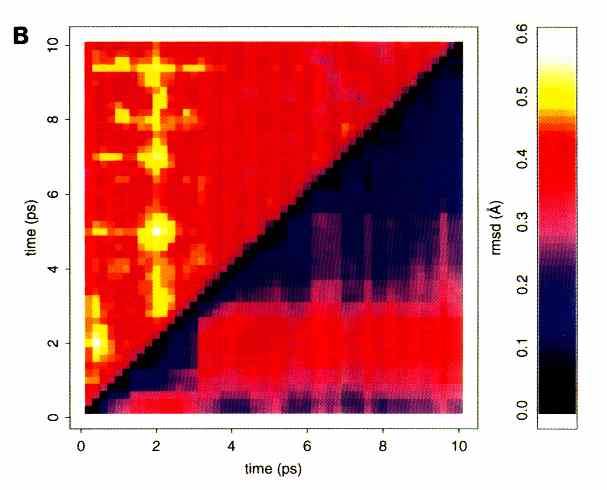
(bal felső rész: MD szerkezetek, jobb alsó: energiaminimalizálás utáni
szerkezetek)
- RMSD: root mean square deviation: az egymásnak megfelelő atomok közötti távolságok négyzetes közepe (a konformációs térben a két konformációnak megfelelő pont távolsága)
- Összefüggő foltok: konformációs klaszterek, alállapotok
- A diagonálistól távol nincsenek fekete részek: a konformáció nem tér
vissza egy korábbi állapotba
- Hierarchikus klaszterezés:
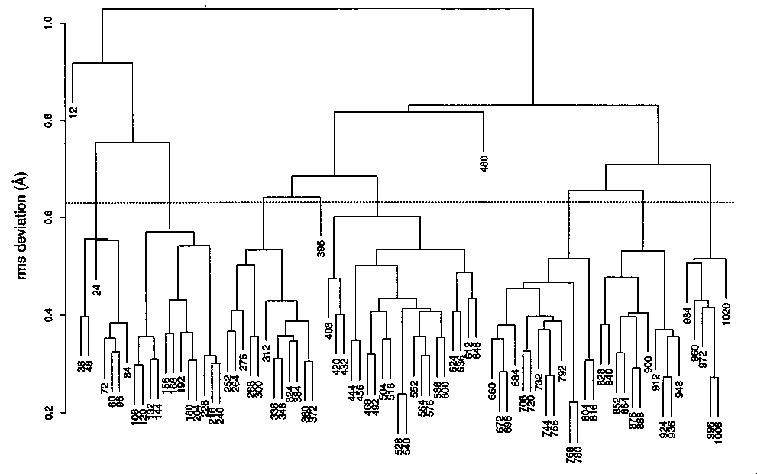
- 7 fő klaszter, alállapot, azaz 7 energiaminimum van, egymástól 0,65
angströmnél messzebb
- Az alállapotokon a szimuláció alatt sorban végigmegy a molekula (nem
elégséges tehát a mintavétel)
- Szerkezetben:

Színek: a 11-18 hurok konformációi a 7 klaszterben
- A legnagyobb változást a 11-18 hurok mutatja: a 14-38 diszulfidhíd mint
tengely körül elfordul kb. 30 fokkal
Tehát: sikerült a natív konformációk halmazán belül alállapotokat
elkülöníteni (7 darabot), a szimuláció során ezeken sorban végigmegy a
molekula. A mintavétel nem elégséges, mert egyetlen korábbi állapot sem áll
elő újra a szimuláció időtartama alatt.
A legombolyodás MD szimulációi
A legombolyítás módozatai
- Magas hőmérséklet (600 K-n 6 nagyságrenddel gyorsabb a legombolyodás,
mint szobahőmérsékleten)
- Nagy nyomás (vízmolekulák benyomulnak a magba)
- Speciális kényszererők
Barnáz legombolyodásának szimulációja
(Li és Daggett, JMB 275:677 (1998))
Barnáz
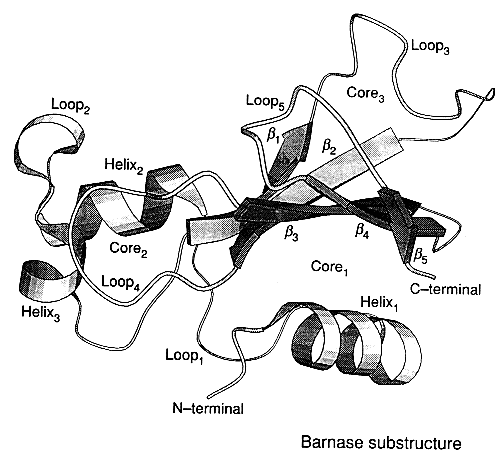
110 aa, 3 hélix, egy ötszálú béta-lemez, 3 hidrofób mag
Szimuláció
- Kiindulás: átlagos NMR-szerkezet
- periodikus határfeltételek, 3700 vízmolekula
- 2000 ps (2 ns) szimuláció 498 K-n
- kontroll: 2 ns szimuláció 298 K-n
Eredmények
- RMSD a kiinduló szerkezettől:
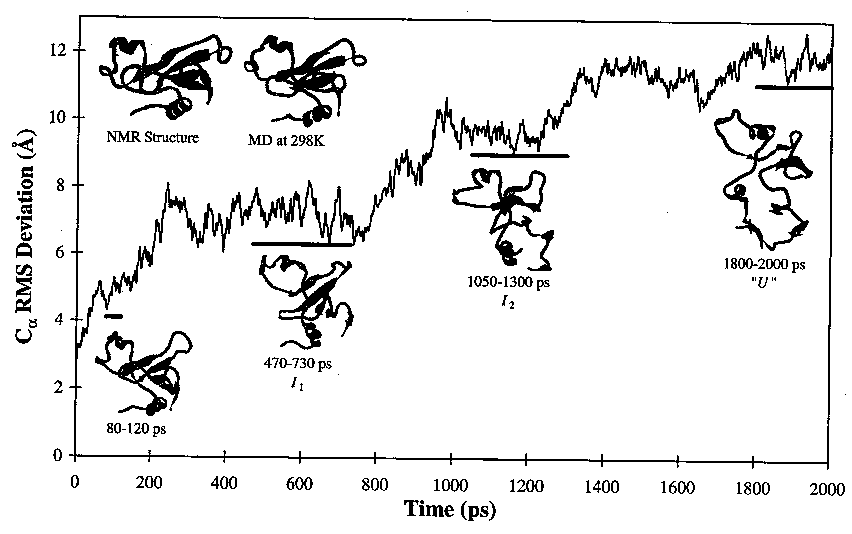
- H-kötések
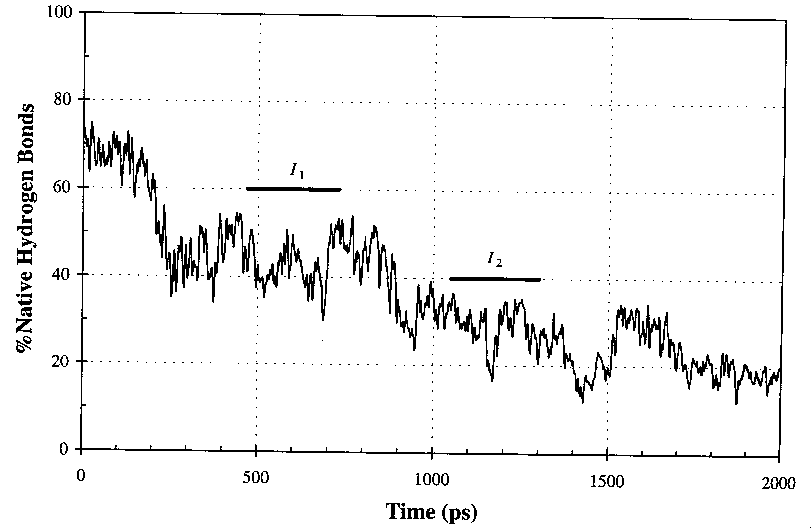
Elemzés
- Két intermedier alakul ki a legombolyodás során, I1 és I2
- I1:
- A 3 hidrofób mag megvan, de fellazultak:
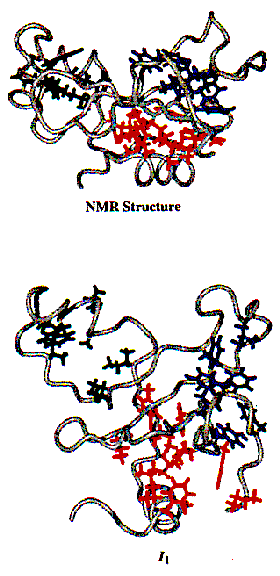
- A béta-lemez közepe megvan, de széle felbomlott:
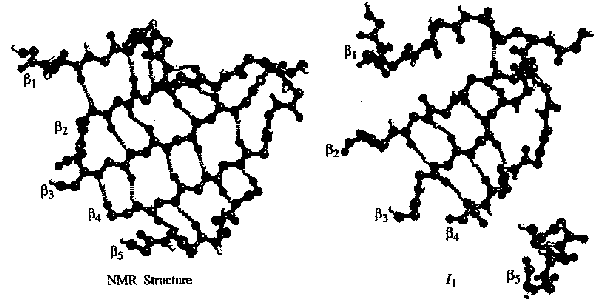
- Másodlagos szerkezet: alfa1 majdnem teljesen megvan, alfa2 első fordulata eltűnt, alfa3 legombolyodott:
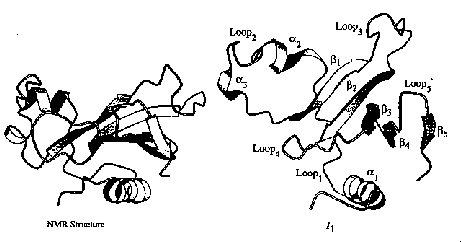
Tehát: a barnáz legombolyodásának szimulációja két köztes
állapotot tárt fel, ez jól egyezik a kísérleti eredményekkel (ld. 6.
előadás), melyek szerint legalább egy köztes állapot van.
Titindomén mechanikus legombolyítása
A molekula
- Titin: 1 mikrométer hosszú molekula simaizom-rostokban, rugóként működik
- Fibronektin-3 és immunglobulin típusú (Ig) domének ismétlődéseiből áll
- A rugalmasságért felelős rész Ig doménekből áll
- Atomierő-mikroszkópiával, ill. lézercsipesszel végzett kísérletekkel
mérték a molekula széthúzásához szükséges erőt. Az erőgrafikon
fűrészfogszerű görbét mutat
Szimuláció
- Egy Ig domén mechanikus széthúzása
- Egyik vég rögzített, másikat 0,5 angström/ps sebességgel húzzák, míg az
egész molekula ki nem egyenesedik
- vízcseppel körülvett domén 300 Celsius-fokon
Eredmények
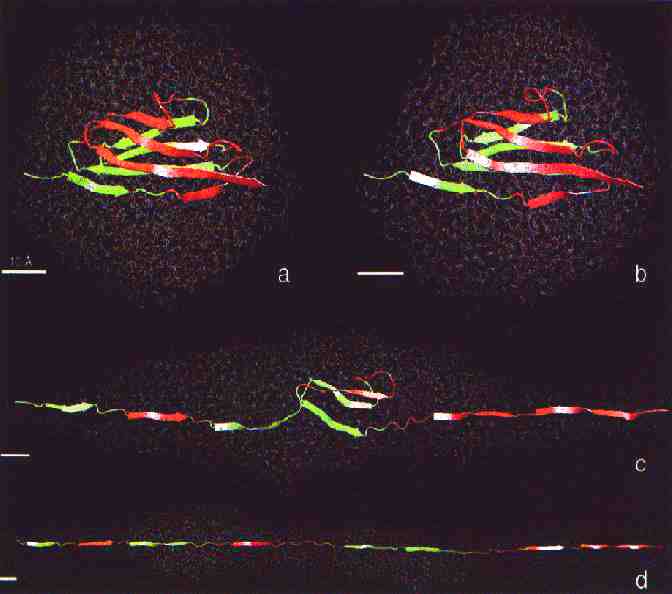
a: 10 angström nyújtás, még semmi nem történt, b: 17
angström nyújtás, az erős ponton túl, c: 150 angström, felerészben
legombolyodott, d: 285 angström, kiegyenesedett
- Mintegy 14 angström széthúzásig a béta-szálak csak elcsúsznak kissé egymás mellett, de megmarad a szerkezet
- 14 angströmnél nagyobb megcsúszás
- ezután a domén fokozatosan legombolyodik, a béta-lemez szálai egyenként leválnak
- 260 angströmnél a molekula kiegyenesedett
- Erőgrafikon:
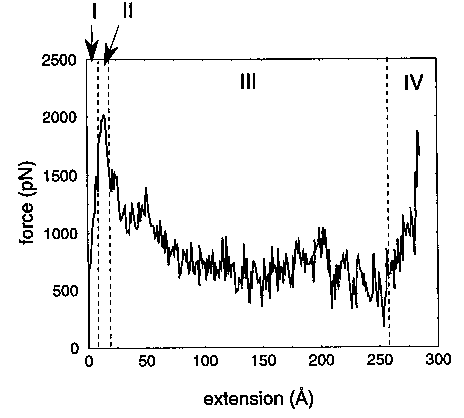
14 anströmig az erő meredeken növekszik, onnét hirtelen lezuhan és nagyjából állandó marad 250 angströmig, ott újra megnő (itt már a kinyújtott molekulát feszítjük)
- Jól egyezik a kísérleti eredményekkel
- Ha sok domén van egymás után, a köztük lévő kis különbségek miatt
egyenként gombolyodnak szét húzás hatására, nem egyszerre.
Tehát: a titindomén mechanikus legombolyításának molekuladinamikai
szimulációja feltárta a legombolyodás mechanizmusát és a kísérletekkel jó
egyezést mutató erőgrafikont szolgáltatott.
A felgombolyodás MD szimulációi
1 mikroszekundumos szimuláció! (rekord mindeddig)
(Duan és Kollman, Science 282:740 (1998)
A fehérje
- HP-36: a villin (egy aktinkötő fehérje) feji részének szubdoménje (36 aminosav)
- önálló felgombolyodásra képes, olvadáspontja >70 fok
- felgombolyodási ideje 10-100 mikrosec közötti (igen rövidnek számít,
ezért választották ezt)
- NMR-szerk: 3 rövid hélix
Szimuláció
- Explicit oldószer (kb. 3000 vízmolekula), periodikus határfeltétel
- Indulás: 1000 K-n 1 ns alatt denaturált fehérjéből
- 1 mikroszekundum szimulációja (kb. 2 hónap processzoridő egy 256
processzoros Cray gépen)
Eredmények
- A szerkezet változásai:
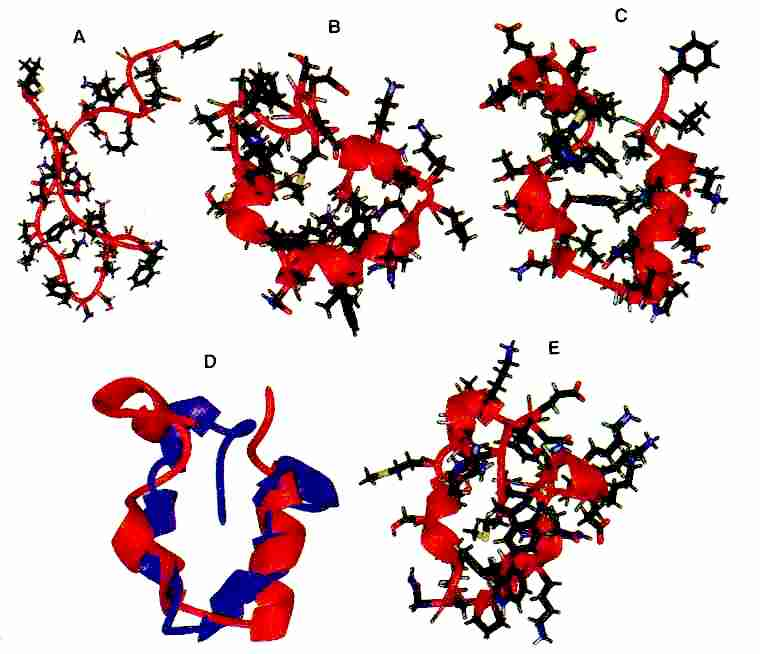
A: kiinduló, C: natív, B: 980 ns-nál, E: a legstabilabb klaszter, D: a
natív (piros) és a legstabilabb klaszter (kék) szerkezet illeszkedése
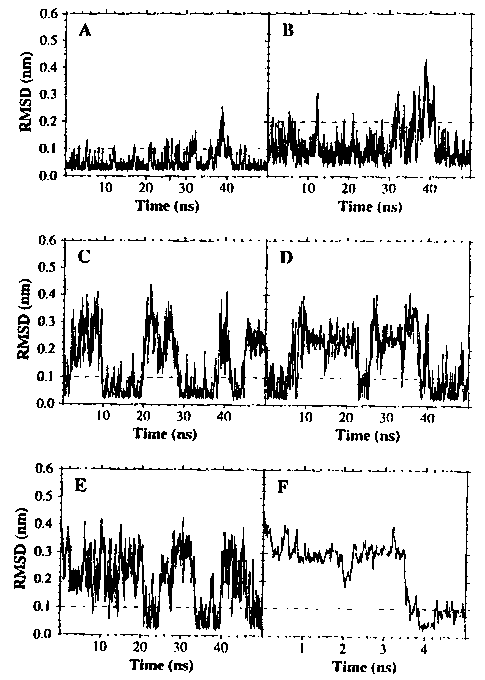
- A paraméterek változásai:
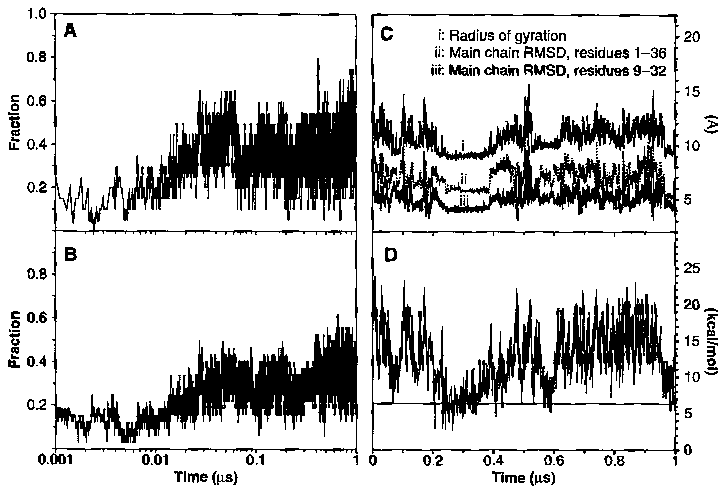
A: hélixtartalom, B: natív kontaktusok hányada, C: girációs sugár és
RMSD-k a natív szerkezettől, D: szolvatációs szabadentalpia (felszínből
számítva). A bal oldali grafikonoknál az időskála logaritmikus, a jobb
oldaliaknál lineáris!
- Két szakasz:
- "burst" fázis: gyors hidrofób kollapszus, hélixképzéssel, kb. 60 ns-on
belül. (Hélixtartalom 0-ról 60%-ra, natív kontaktusok aránya 3%-ról 45%-ra
nő, szolvatációs szabadentalpia 14 kcal/mol-lal csökken (natívközeli szintre).
- lassabb, átrendeződési fázis: hélixtartalom kb. 20%-ra csökken,
mindegyik paraméter erősen fluktuálni kezd. Kb. 200 ns-től lassú növekedés a
hélixtartalomban és a natív kontaktusok arányában
- Egy stabil állapot: 240 és 400 ns között egy szokatlanul stabil
(160 ns életidejű) állapot lép fel. Girációs sugár és rmsd közel állandó,
szolvatációs szabadentalpia igen alacsony. Nagyon hasonlít a natív
szerkezetre.
- Klaszteranalízisből: ehhez a stabil állapothoz 3 út vezet
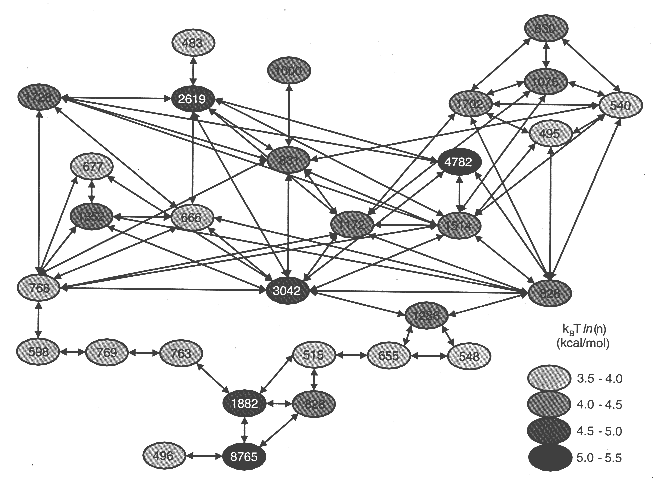
A felgombolyodás útvonalai. Az ellipszisek a főbb klasztereket
reprezentálják, a nyilak az átmeneteket köztük. Az ellipszisekben lévő
számok a klaszterekben lévő szerkezetek számát jelzik. A 240 és 400 ns
közötti stabil állapot alul a 8765 szerkezetet tartalmazó, legnépesebb
klaszter.
Tehát: a felgombolyodás molekuladinamikai szimulációja a
kísérletből ismert natív szerkezethez közeli szerkezetet eredményezett,
időbeli lefutása jó egyezést mutat a felgombolyodás kísérletből ismert
menetével (gyors hidrofób kollapszus és másodlagosszerkezet-képzés, majd
lassú átrendeződés) és sajátosságaival (több lehetséges útvonal).
Folding at home: felgombolyítás otthon
A Stanford egyetem elindította a Folding at home projektet.
Mikroszekundumnál hosszabb felgombolyodási szimulációt végeznek olyan módon,
hogy a számítási munkát szétosztják az interneten lévő számítógépek között.
Bárki letöltheti és képernyővédőként futtathatja azt a programot, ami a
szimuláció egy részét végzi, így egy sok ezer processzoros, a világ minden
részére elosztott, virtuális szuperszámítógép végzi a szimulációt.
Lásd:
http://foldingathome.stanford.edu/