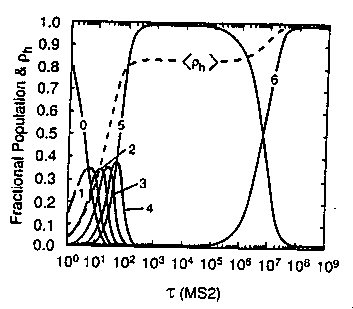
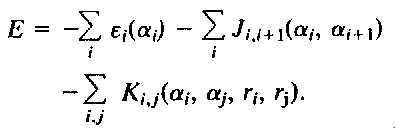A rácsmodell. Szabadenergia-felületek.
1. A spinüveg-modell
2. A rácsmodellek típusai
3. A rácsmodellek előnyei és hátrányai
4. A rácsmodellek elemzése
5. Egyszerű rácsmodellek
6. Rácsmodellek natív állapotai
7. Oldalláncok
8. Rácsmodellek felgombolyítása
9. Szabadenergia-felületek
10. A rácsmodellek következtetései
A spinüveg-modell
(Bryngelson és Wolynes 1987)
- Megfigyelés: a fehérjék bonyolultan viselkednek:
- Egyes fehérjék
fázisátalakulás-szerűen, éles átmenetben gombolyodnak fel, mások köztes
állapotokkal (félregombolyodott állapotok, olvadt gombócok).
- A felgombolyodás kinetikája komplex, multiexponenciális, időben sok
nagyságrendet ölel fel. A lassú felgombolyodás sok lokális energiaminimum
jelenlétére utal.
- Előfordul irreverzibilis denaturáció, a fehérjék "öregedése".
- Mindez emlékeztet az üvegek tulajdonságaira
- Spinüveg: Mágneses spinekből álló rendszer, véletlenszerűen
elosztott ferromágneses (spineket párhuzamosan beállítani igyekvő) és
antiferromágneses (spineket ellentétesen beállítani igyekvő) kölcsönhatásokkal
- A spinüvegek jellemzői:
- Bonyolult, sok lokális minimummal rendelkező energiafüggvény
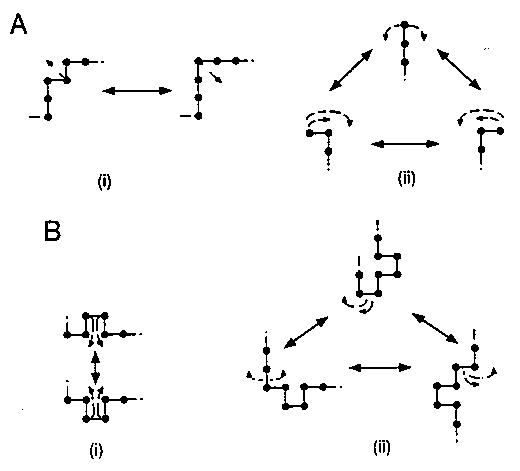
- Frusztráció: A kölcsönhatások csatoltsága miatt nem lehet
mindegyik kölcsönhatást egyszerre kielégíteni. (Pl. három spinből álló
rendszer, mindegyik pár között antiferromágneses kapcsolattal.)
- Üvegátmenetek. A hőmérséklet csökkentésekor a rendszer
valamelyik lokális energiaminimumba befagy. Hogy melyikbe, az a rendszer
előtörténetétől, ill. részben a véletlentől függ.
- Bryngelson és Wolynes modellje: A fehérje energiafüggvénye
(egyszerűsített modellre értelmezve):
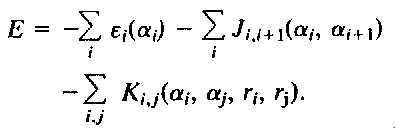
ahol epsziloni(alfai) az alfa állapotban lévő, i-edik
aminosav saját energiája,
Ji,i+1(alfai,alfai+1)
két szomszédos aminosav kölcsönhatása (lokális kölcsönhatás),
Ki,j(alfai,alfaj,ri,rj)
a távol lévő i. és j. aminosav (nemlokális) kölcsönhatása, amely a
helykoordinátáiktól is függ. Ez matematikailag egy spinüveg energiafüggvénye.
- Az elemzésből adódik a fehérjék fázisdiagramja:
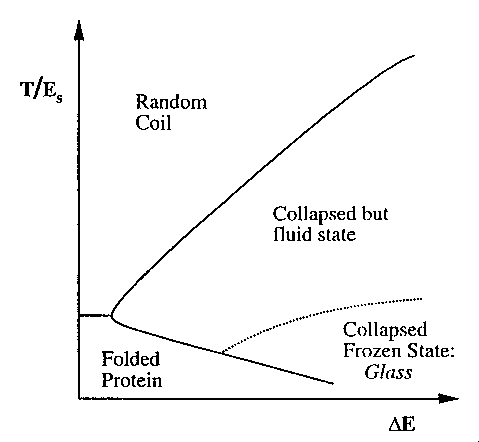
deltaE: az energiafelület hepehupássága, T: hőmérséklet, ES:
stabilitási hézag: a natívközeli és attól távoli állapotok közötti
energiakülönbség
A fázisdiagramon szerepel a teljesen legombolyodott állapot (random coil), a
felgombolyodott állapot, valamint az összeesett, de képlékeny állapot
(egyfajta olvadt gombóc). Alacsony hőmérsékleten, nagy hepehupásság esetén
fellép egy negyedik állapot: üvegszerűen befagyott állapot.
- Az üvegállapot kísérletek szerint számos fehérjénél fellép 200 K körüli
hőmérsékleten (a konformációs fluktuációk jellege megváltozik).
- Frusztráció a fehérjékben: számos kölcsönhatásnak (hidrofób
kontaktusok, hidrogénkötések, stb.) kellene egyszerre létrejönni, ami
lehetetlen.
- Minimális frusztráció elve (Bryngelson és Wolynes): a natív
állapot az, amelyik minimális mértékben frusztrált. A szekvenciatérben
értelmezve: a minimálisan frusztrált szekvenciák képesek jóldefiniált natív
szerkezetet felvenni.
- Az energiafelület hepehupássága: A fehérjék egyszerre mutatják az
egyszerű rendszerek és a komplex, spinüveg-szerű rendszerek tulajdonságait.
Magyarázat: a felgombolyodásképes fehérjék energiafelületén a lokális
minimumok nem véletlenszerűen helyezkednek el, mint a spinüvegeknél
általában, hanem egy durva oldalú tölcsért képeznek, amely viszonylag
hatékonyan vezérli a rendszert a natív állapotnak megfelelő minimum felé.
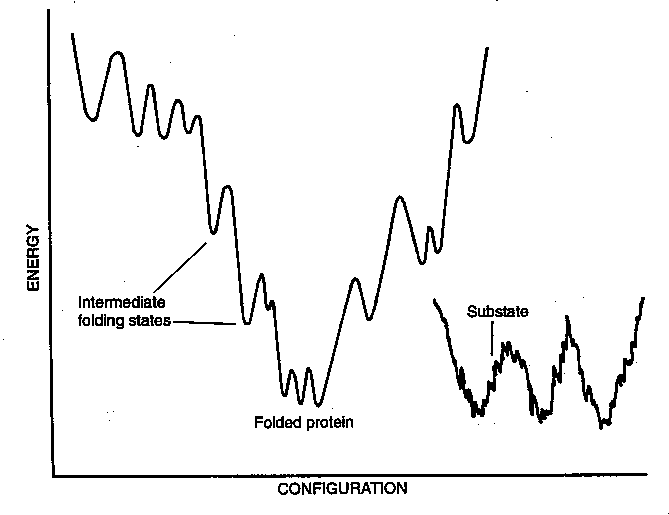
- Ez a kép alapozta meg a felgombolyodás "új szemléletét", s ez inspirálta
a 90-es évek elejétől a rácsmodellek kifejlesztését.
A rácsmodellek típusai
Rácsmodell: "önelkerülő" gyöngysor, rácspontokon
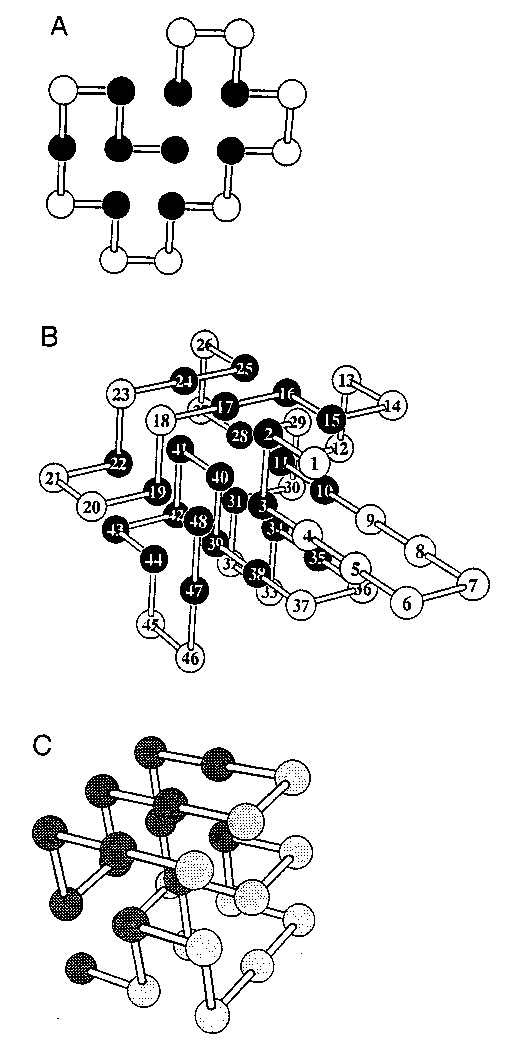
A: 2D HP modell, B: 3D HP modell, C: Perturbált heteropolimer modell,
kétbetűs kóddal
- HP modell (Hidrofób-Poláros) [Ken A. Dill és mások]
- Kétféle aminosav: Hidrofób és Poláros (kétbetűs kód)
- 2D és 3D modellek. Eredményeik hasonlóak; a 2D modellek
könnyebben számíthatóak. Hidrofób maggal rendelkező modell 2d-ben 16, 3D-ben
64 aminosavból készíthető.
- Egyparaméteres: epszilon kontaktenergia (a HH kontaktus energiája)
- A kontaktusok energiája:
(EHH, EHP,
EPP)=(-epszilon, 0, 0)
- Perturbált heteropolimer modellek [Eugene I. Shakhnovich és mások]
- Erős vonzás a monomerek között, gyenge variációval
- Többnyire 27-mer, alapállapota 3x3x3-as kockán (103 346 lehetséges
állapot)
- Két változat:
- Független kontaktenergiák: E(i,j)=Bi,j
- Kétbetűs kód: A,B. Ált.
EAB>EAA,EBB. (Ált. nem mag-felszín
szeparációhoz, hanem jobb-bal elkülönüléshez vezet.)
- Bírálat Dilltől: nem elég jó modell (valódi fehérjékre nem teljesülnek a
felsorolt tulajdonságok)
 | 
|
| Ken Dill (UCSF) | Eugene Shakhnovich (Harvard)
|
A rácsmodellek előnyei és hátrányai
Előnyök
- Szekvenciatér és konformációtér teljességében felderíthető
- Egzaktul kiszámítható mennyiségek! (Jobb az egyszerű, de egzaktul
számolható modell, mint a bonyolult, de csak közelítőleg számítható.)
- Nem csak fehérjékre vonatkoztatható
- Használható analitikus elméletek tesztelésére (mint spinüveg-modell,
átlagtér-elméletek)
- Használható konformációkereső algoritmusok tesztelésére
Hátrányok
- Az atomi felbontás hiánya
- A szerkezeti és energetikai részletek nem pontosak
- A lánc sokszor irreálisan rövid
A rácsmodellek elemzése
- Enumeráció: a modell összes lehetséges állapotának előállítása,
megszámlálása és jellemzése. Kisebb modelleknél járható.
- Monte Carlo mintavétel: Monte Carlo módszerrel (véletlenszerű
generálás) véletlen állapotok
előállítása, ebből statisztikai számítás. Nagyobb modelleknél.
(Hibalehetőségek vannak, pl. rossz becslésekből.)
- A natív állapot megkeresése: Kisebb modelleknél az összes
lehetséges állapot végigpróbálásával, nagyobbaknál becslés speciális
algoritmusokkal. A HP modellek alapállapotának megkeresése ún. NP-nehéz
feladat (a megoldáshoz szükséges idő a lánchossznak nem polinomiális
[hanem annál gyorsabban növekvő] függvénye).
Egyszerű rácsmodellek
Négytagú játékmodell
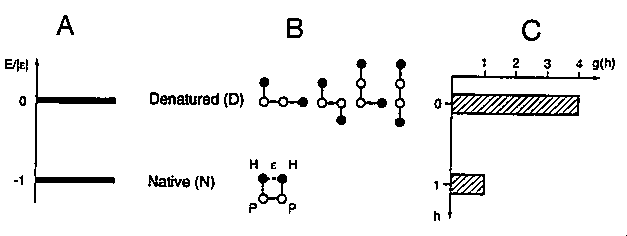
A: energiaszintek, B: állapotok, C: h kontaktushoz tartozó
állapotok száma, g(h)
- Legegyszerűbb 2D HP rácsmodell, szekvencia: HPPH
- h db kontaktusnál az energia -h epszilon
- Termodinamikai jellemzés:

- A paraméterek hőmérsékletfüggése:
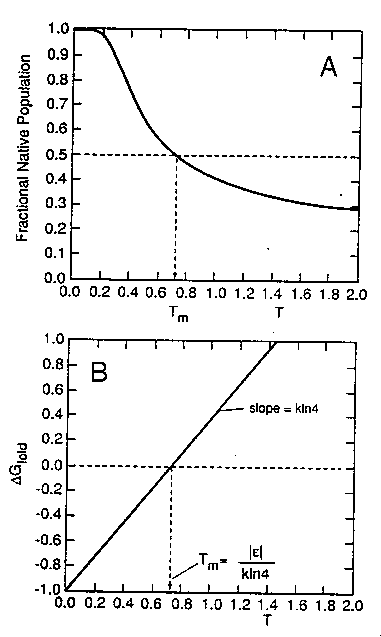
A: Natív populáció részaránya, B: deltaG
felgombolyodási szabadentalpia. Tm olvadáspontnál a natívhányad
50%, a szabadentalpia nulla. A szabadentalpia-függvény lineáris (valódi
fehérjéknél görbült)
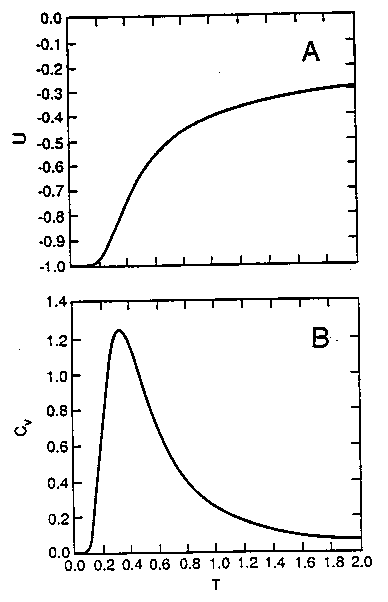
A: energia, B: hőkapacitás. A
hőkapacitás-görbe jellegzetes átmeneti csúcsot mutat
- Már ez a legegyszerűbb modell is mutatja a fehérjék egyes termodinamikai
tulajdonságait
Hattagú játékmodell
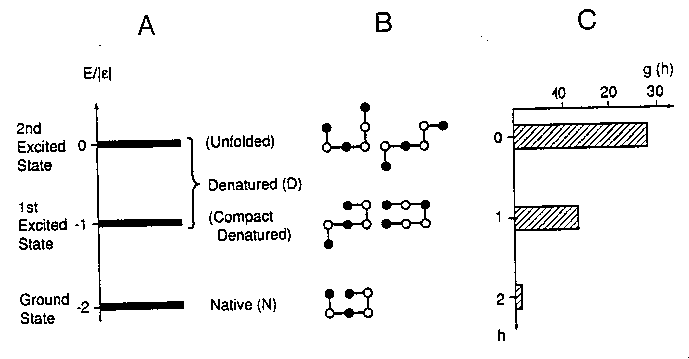
A: energiaszintek, B: néhány állapot (nem az összes!), C:
állapotsűrűség-függvény
- Hattagú 2D HP modell, szekvencia: HPHPPH
- Termodinamikai elemzés: mint a négytagúnál
- Három energiaszint: három állapot
- Populációeloszlások a hőmérséklet függvényében:
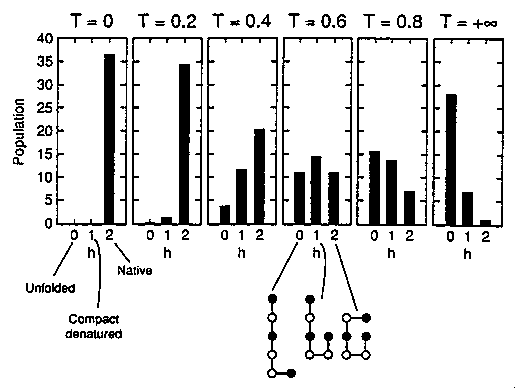
A populáció a tisztán natív állapotból indulva a köztes állapoton át
folyamatosan áttolódik a denaturált állapotra
- Felgombolyodási szabadentalpia a hőmérséklet függvényében:
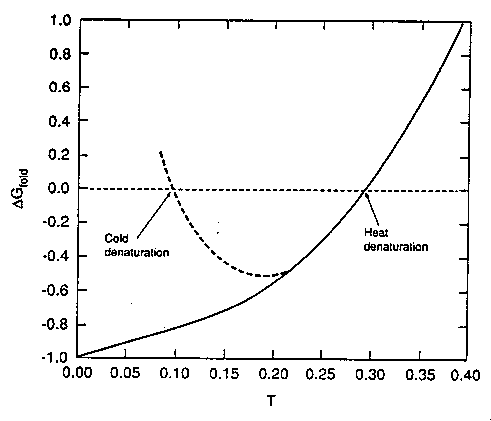
Az intermedier állapot miatt már nem lineáris, hanem görbül, mint a
valódi fehérjéknél. Ha epszilont hőmérsékletfüggővé tesszük (a hőmérséklet
csökkenésével csökken, akárcsak a hidrofób kölcsönhatás), a szaggatott
vonallal jelzett görbét kapjuk. Ez mutatja a valódi fehérjékre jellemző,
parabolaszerű görbét, a hidegdenaturációval.
- Egy egyszerű hattagú modell már a fehérjék szabadentalpia-görbéjét is
jól modellezi
Húsztagú modellek
A szekvenciától függően sokféle viselkedés:
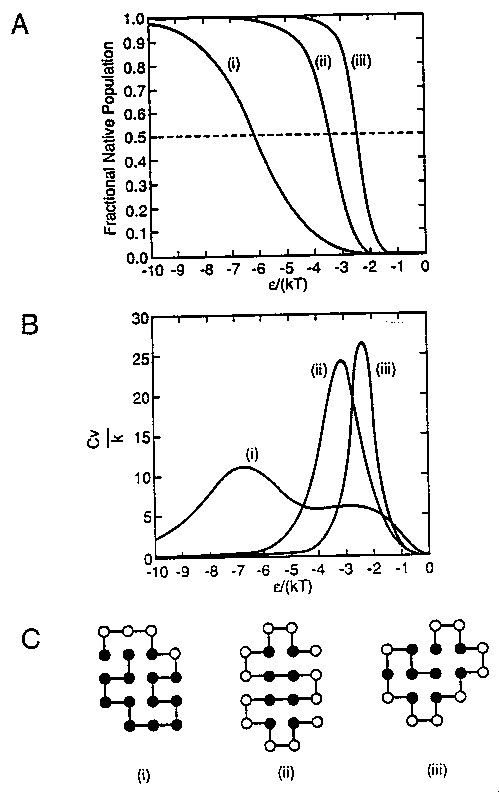
A: natív részarány, B: hőkapacitás, epszilon/kT függvényében, C: a
modellek natív állapotai (legmélyebb energiaszint)
- epszilon a hidrofób kölcsönhatás erősségét jellemzi, epszilon/kT a
denaturálószer-koncentrációnak feleltethető meg
- (ii) és (iii) fehérjék éles átmenetet mutatnak, (i) kétcsúcsú,
széles átmenetet: kétdoménes fehérje
- A (ii) modell populációeloszlása a hőmérséklet függvényében:
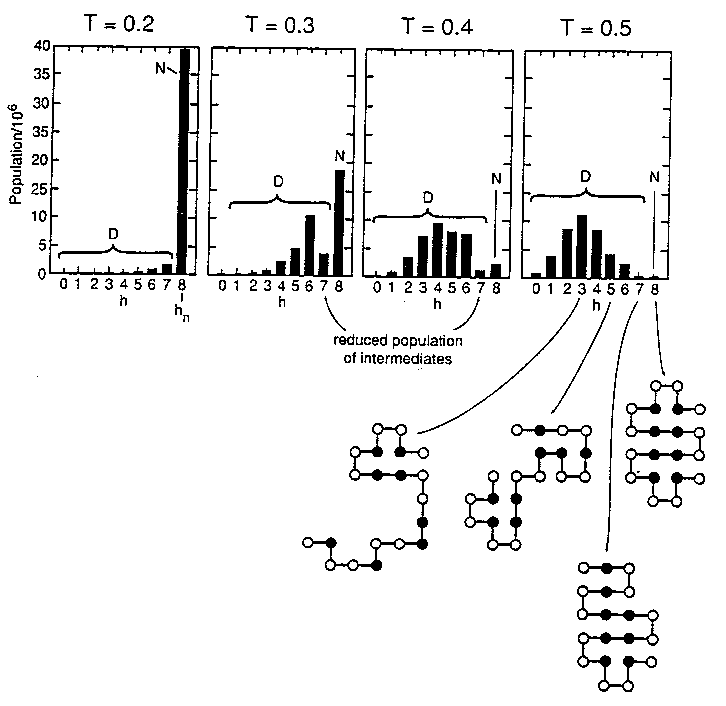
T=0,3-nál és T=0,4-nél a natív (N) és denaturált (D) populációk jelentősek,
köztük jelentéktelenebb populáltságú köztes állapottal (az eloszlásnak
minimuma van). Ez a kétállapotú kooperativitás.
- Egy húsztagú modell már kétállapotú kooperativitást képes mutatni, mint
a valódi fehérjék
- A modell natív állapota egy béta-lemezt és két hélixet tartalmaz,
hidrofób maggal, poláros felszínnel
Rácsmodellek natív állapotai
- Nem minden HP szekvenciának van egyetlen natív állapota (egyetlen natív
állapot: gN=1)
- Adott hosszúságú HP szekvenciák közül az egyetlen natív állapottal
rendelkezők százalékos aránya:
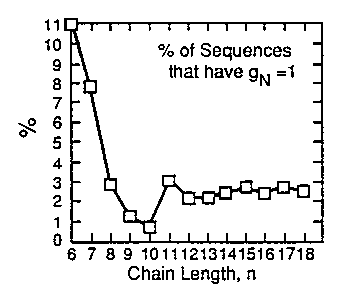
A 10-nél hosszabb szekvenciáknak csak mintegy 2-3%-a rendelkezik egyetlen
natív állapottal. Tehát igen speciális szekvenciákról van szó.
Egyetlen natív állapottal rendelkező szekvenciák
tervezése
- Adott térszerkezethez könnyű olyan szekvenciát tervezni, amelynek a
térszerkezet alacsony energiájú állapota
- Jóval nehezebb viszont biztosítani, hogy az adott szekvencia ne vehessen
fel más, szintén alacsony vagy még alacsonyabb energiájú állapotot. Ez a
negatív tervezés.
- Példa:
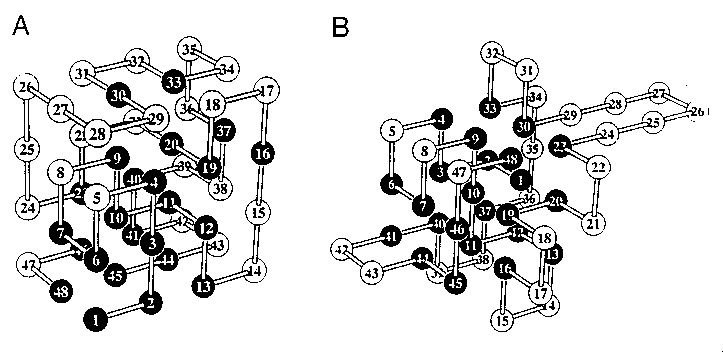
A: Shaknovichék tervezte szekvencia a képen látható térszerkezetre. Monte
Carlo módszerrel dolgozva csak a maximálisan kompakt (kocka formájú)
állapotokat vizsgálták
B: Dillék a saját kereső algoritmusukkal kimutatták, hogy az adott
szekvenciának van egy még alacsonyabb energiájú állapota, ami viszont nem
maximálisan kompakt
- 20 aminosav esetén az egyetlen natív állapotot könnyebb megvalósítani,
mint 2-nél
Oldalláncok
Mi az oldalláncok szerepe a natív szerkezet specificitásának
meghatározásában?
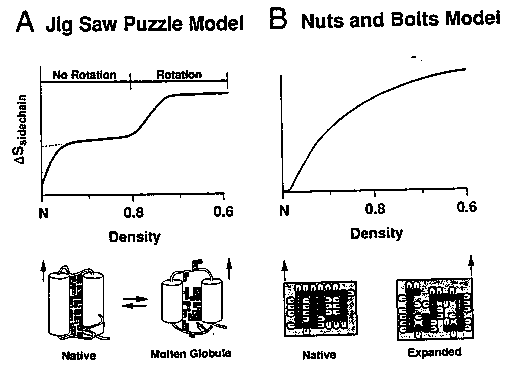
- Puzzle-modell: A natív térszerkezetet az tünteti ki, hogy az
oldalláncok pontosan illeszkednek, mint egy puzzle darabjai. Az olvadt
gombóc állapot lényege az, hogy már kész a szerkezet, csak még az
oldalláncok összeilleszkedése hiányzik
- Csavarok és anyák modell: Az oldalláncok nem kirakós játék
részeiként illeszkednek, hanem úgy töltik ki a teret, mint egy dobozban egy
rakás csavar és anya, vagyis nem specifikusan; átrendeződések lehetségesek
- Illusztráció:
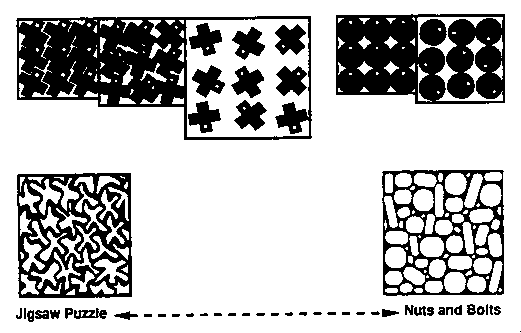
- Melyik modell igaz? Shaknovichék szerint a puzzle, Dillék szerint
a "csavarok és anyák"
- Eldöntés: Hogyan függ az oldalláncok entrópiajáruléka a kompaktságtól?
- Puzzle-modell: A molekulát tágítva a szoros illeszkedés miatt jó ideig
semmi sem történik, majd egy ponton ugrásszerűen megnő az oldalláncok
rotációs szabadsága
- Csavarok és anyák: Tágításkor folyamatosan nő az oldalláncok rotációs
szabadsága, nincs ugrásszerű változás
- Kísérleti adatok mindkét modell mellett és ellen felhozhatóak
- Vizsgálat rácsmodellel: oldalláncokkal bővített rácsmodell
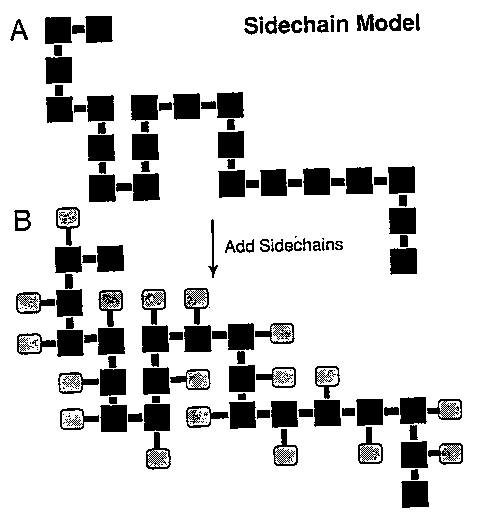
- Ezekkel dolgozva az oldalláncok entrópiajáruléka a kompaktság
függvényében:
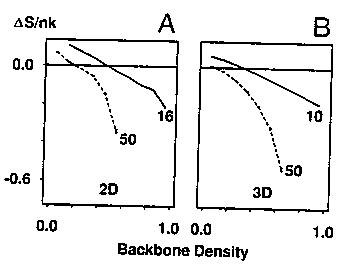
A: 16 és 50 tagú 2D HP modellek, B: 10 és 50 tagú 3D HP modellek
- Eredmény: A kompaktság növelésével rohamosan csökken az entrópia,
befagynak az oldalláncok. Az oldalláncok és a gerinc szabadsági fokai erősen
csatoltak; csak az oldalláncaiban megolvadt gombóc nem képzelhető el.
Ez a "csavarok és anyák" modellt támasztja alá.
Rácsmodellek felgombolyítása
Mutációk hatása a felgombolyodásra
Hogyan hat egy H-->P mutáció a felgombolyodás sebességére?
Két azonos natív szerkezetű, csak egy elemben eltérő HP modellben
mutációt végzünk (az eltérő elemtől távol):
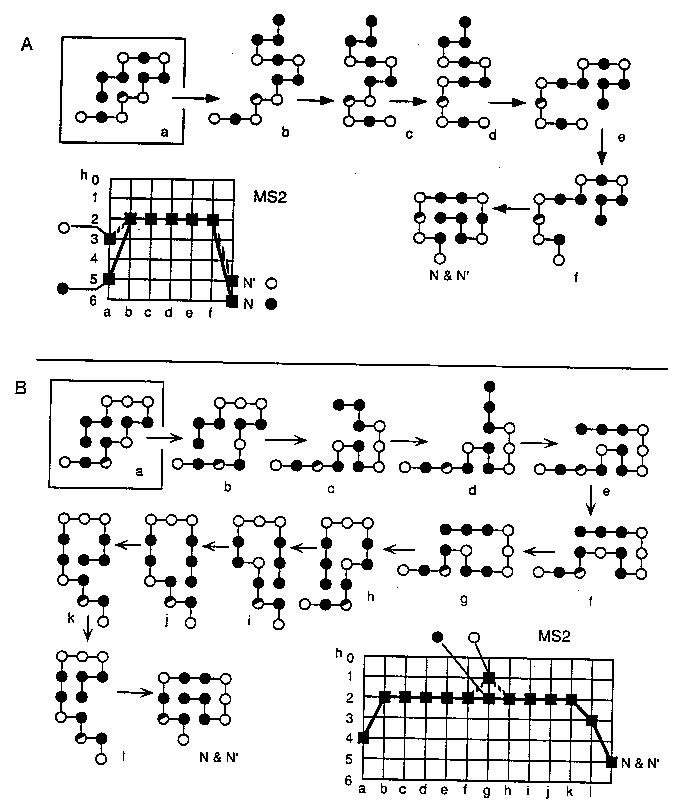
- A: A mutáció gyorsítja a felgombolyodást, mert a felgombolyodás útvonalán
a vad típusban fel kell szakítani egy HH kötést, a mutánsban viszont nem.
- B: A mutáció lassítja a felgombolyodást, mert a felgombolyodás útvonalán
a vad típusban a H segít felbontani egy nemnatív HH kontaktust, a mutánsban
a P ezt nem tudja megtenni, nő az energiagát nagysága.
Tehát ugyanolyan típusú mutáció lassíthatja vagy gyorsíthatja is a
felgombolyodást, ahogy a valódi fehérjéknél is.
Szabadenergia-felületek
Rácsmodellek Monte Carlo szimulációiból számítható a szabadenergia:
F=E-TS
ahol E az energia (a kontaktusok számából), S az entrópia (az adott
energiájú állapotok számából számítható).
A szabadenergiát megfelelő mennyiségek mint koordináták függvényében
ábrázolva szemléletes felületek adódnak. Ilyen mennyiségek pl.:
- C: az összes kontaktusok száma
- Q0: a natív kontaktusok száma (olyan kontaktus, ami a natív
szerkezetben is megvan)
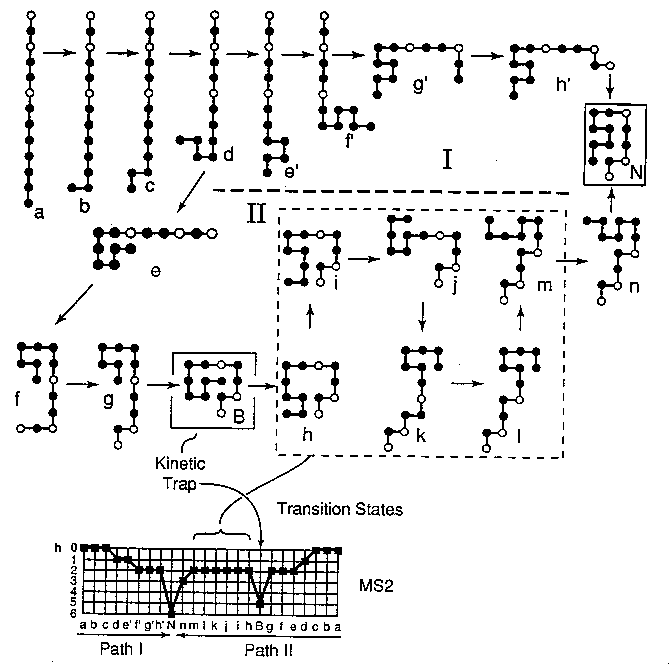
Egy 27 elemű rácsmodell szabadenergia-felülete
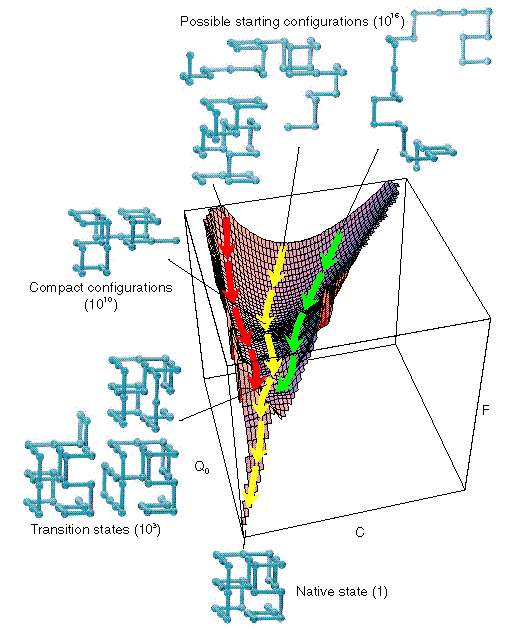
A szimuláció menete ezen a felületen szemléltethető:
- A szimuláció random szerkezetből indul (kevés kontaktus): hozzáférhető
állapotok száma kb. 1016
- Gyorsan összeesik egy kompakt szerkezetté, mely a lehetséges kontaktusok
60%-át tartalmazza, de a 60%-nak csak 25%-a natív kontaktus. A
hozzáférhető állapotok száma kb. 1010.
- Itt egy széles minimum van a szabadenergiában
- Ezután lassú folyamat következik: a lánc keresi a natív állapot felé
vezető átmeneti állapotot
- Átmeneti állapotok száma 103
- Az átmeneti állapotból gyorsan betalál a natívba (1 állapot)
- Zöld, piros: lehetséges, különböző útvonalak. Sárga: átlag.
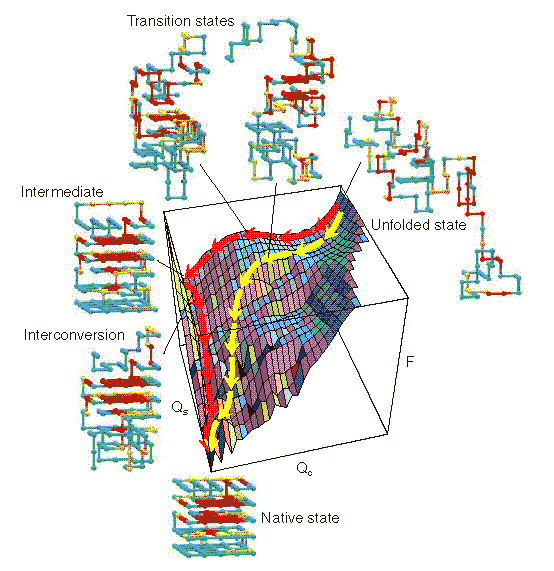
A lizozim szabadenergia-felülete
A lizozim felgombolyodásának menete kísérletből ismert. Ennek alapján
szerkeszthető egy hipotetikus energiafelület, melynek koordinátái:
Qalfa és Qbéta: a natív kontaktusok száma az alfa,
ill. béta doménben. A felület:
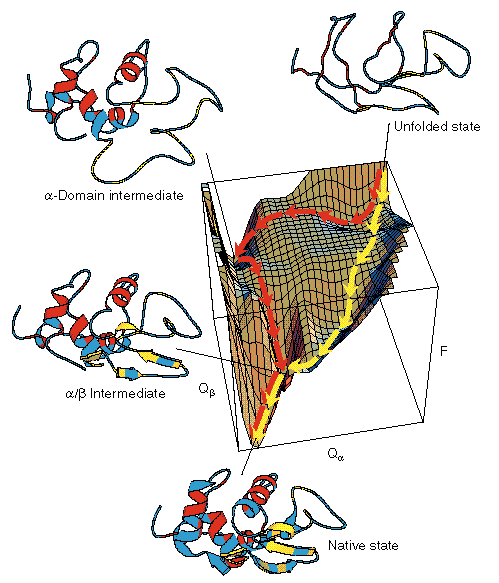
- A molekulák kb. 20%-a gyorsan felgombolyodik (sárga útvonal, <100 ms
időállandó), natívszerű intermedierrel
- A molekulák kb. 70%-a jóval lassabban gombolyodik fel (piros útvonal,
kb. 400 ms időállandó), olyan intermedierrel, amely csak az alfa doménben
natívszerű
- A molekulák 10%-a nagyon lassan gombolyodik fel (prolinizomerizáció
miatt, ezt nem jelöltük)
- Mindegyik út utolsó lépése a két, már kialakult domén asszociációja
Egy 125 elemű rácsmodell szabadenergia-felülete